题目内容
【题目】在![]() 中,
中,![]() 是锐角,过
是锐角,过![]() 两点以
两点以![]() 为半径作
为半径作![]()
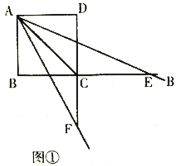
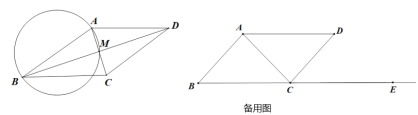
(1)如图,对角线![]() 交于点
交于点![]() ,若
,若![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的值
的值
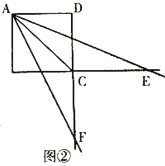
(2)![]() 与边
与边![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 的长为
的长为![]() ,当
,当![]() 时,求
时,求![]() 的度数(提示:可再备用图上补全示意图)
的度数(提示:可再备用图上补全示意图)
【答案】(1)1;(2)90°
【解析】
(1)先证得![]() 为菱形,由菱形的性质得到AC⊥BD,从而判断出线段AB为
为菱形,由菱形的性质得到AC⊥BD,从而判断出线段AB为![]() 的直径,从而得到r.
的直径,从而得到r.
(2)依题意补全图形,结合图形,证明点D在圆上,得到DF为直径即可求解.
(1)解:在□ABCD中,AB=BC=2,
∴四边形ABCD是菱形.
∴AC⊥BD.
∴∠AMB=90°
∴AB为⊙O的直径
∴r=![]() AB=1
AB=1
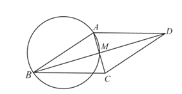
(2)解:连接AE,设圆心为如图点O,连接OA,OB,OC,OD,OE,直线OC与AD交于点N,则OA=OB=OE=r.
在⊙O中,![]() =
=![]() .
.
∵![]() =
=![]() r,
r,
∴ n=90°.即∠AOE=90°,
∴∠ABE=![]() ∠AOE=45°.
∠AOE=45°.
在□ABCD中,AD∥BC,
∴∠ACB=∠DAC=45°.
∴∠ABE=∠ACB=45°.
∴∠BAC=90°,AB=AC.
∴在Rt△ABC中,BC=![]() =
=![]() AB.
AB.
∵CE=![]() AB,
AB,
∴BC=CE.
又∵OB=OE,
∴OC⊥BE
∴∠OCB=90°
∵AD∥BC,
∴∠OCB=∠ONA=90°.
∴OC⊥AD.
在□ABCD中,∠ADC=∠ABC=45°.
∴∠DAC=∠ADC =45°.
∴AC=CD.
∴AN=ND
即直线OC垂直平分AD
∴OA=OD.
∴点D在⊙O上
∴DF为⊙O的直径.
∴∠DEF=90°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目