题目内容
【题目】某校为了调查学生预防“新型冠状病毒”知识的情况，在全校随机抽取了一部分学生进行民意调查，调查结果分为A．B．C三个等级，其中A：非常了解，B：了解，C：不了解，并根据调查结果绘制了如下两个不完整的统计图，请根据统计图，解答下列问题：
（1）这次抽查的学生为 人；
（2）求等级A在扇形统计图中所占圆心角的度数；
（3）若该校有学生2200人，请根据抽样调查的结果，估计该校约有多少学生对预防新型冠状病毒知识已经了解．
【答案】（1）500；（2）118.8°；（3）1958名
【解析】
（1）根据B等级人数以及百分比求出总人数；
（2）先求出A等级人数，然后用360°×A等级人数占总数的百分比即可解决问题．
（3）利用样本估计总体的思想，用2200×（A等级与B等级对应的百分比之和）即可解决问题即可．
解：（1）280÷56%=500人
故答案为：500；
（2）A等级人数为：500-280-55=165
∴A等级所占圆心角度数为：
（3）
人
答：该校约有1958名学生对预防新型冠状病毒知识已经了解．
【题目】如图，
是直径
所对的半圆弧，点
是与直径所围成图形的外部的一个定点，
，点
是上一动点，连接
交于点
．
小明根据学习函数的经验，对线段
，
，
，进行了研究，设
，两点间的距离为
，，两点间的距离为
，，两点之间的距离为
．
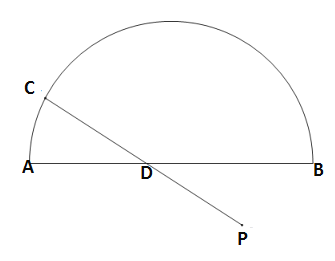
小明根据学习函数的经验，分别对函数
，随自变量
的变化而变化的规律进行了探究．
下面是小明的探究过程，请补充完整：
（1）按照下表中自变量的值进行取点、画图、测量，分别得到了，
与的几组对应值：
| 0.00 | 1.00 | 2.00 | 3.00 | 3.20 | 4.00 | 5.00 | 6.00 | 6.50 | 7.00 | … |
| 0.00 | 1.04 | 2.09 | 3.11 | 3.30 | 4.00 | 4.41 | 3.46 | 2.50 | 1.53 | … |
| 6.24 | 5.29 | 4.35 | 3.46 | 3.30 | 2.64 | 2.00 |
| 1.80 | 2.00 | … |
写出表格中
的值，
_______________________（保留两位小数）；
（2）在同一平面直角坐标系
中，画出函数的图象：
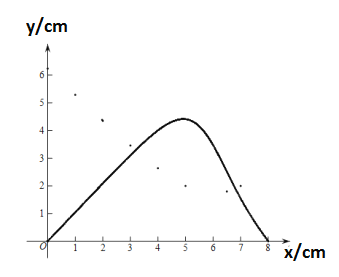
（3）结合函数图象解决问题：当
时，的长度约为_____________________．
