题目内容
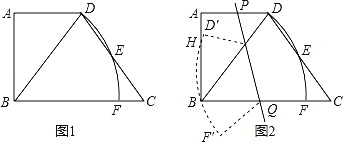
【题目】如图,六边形![]() 是正六边形,点
是正六边形,点![]() 是边
是边![]() 的中点,
的中点,![]() 分别与
分别与![]() 交于点
交于点![]() ,则
,则![]() 四边形MCDN的值为( )
四边形MCDN的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
设BE的中点为O,则O为正六边形ABCDEF的中心,过点O作OQ⊥CD于Q,连接AC交BE于G,连接FD交BE于H,根据六边形![]() 是正六边形得到正六边形的边长都相等,各内角都相等,都等于120°,从而得到∠BAC=∠BCA=30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG,所以∠CAF=∠AFD=∠CDF=∠GCD=∠OGC=90°,根据直角三角形中30°所对的边等于斜边的一半,得到AB=2BG,可以得到四边形ACDF和四边形OGCQ都是矩形,所以AF∥GH∥CD,AF=GH=CD,OQ=CG=AG,设BG=a,则AB=2a,AP=
是正六边形得到正六边形的边长都相等,各内角都相等,都等于120°,从而得到∠BAC=∠BCA=30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG,所以∠CAF=∠AFD=∠CDF=∠GCD=∠OGC=90°,根据直角三角形中30°所对的边等于斜边的一半,得到AB=2BG,可以得到四边形ACDF和四边形OGCQ都是矩形,所以AF∥GH∥CD,AF=GH=CD,OQ=CG=AG,设BG=a,则AB=2a,AP=![]() AF=
AF=![]() AB=
AB=![]() ×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a,根据GM∥AP得到△CGM∽△CAP和△DHN∽△DFP,可得GM=
×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a,根据GM∥AP得到△CGM∽△CAP和△DHN∽△DFP,可得GM=![]() AP=
AP=![]() a,NH=
a,NH=![]() PF=
PF=![]() a,根据线段的和差可以求出BM,MN,AG,CD的长,根据三角形面积公式和梯形面积公式即可求出S△PBM和S四边形MCDN的面积,从而得到它们的比值.
a,根据线段的和差可以求出BM,MN,AG,CD的长,根据三角形面积公式和梯形面积公式即可求出S△PBM和S四边形MCDN的面积,从而得到它们的比值.
解:设BE的中点为O,则O为正六边形ABCDEF的中心,过点O作OQ⊥CD于Q,连接AC交BE于G,连接FD交BE于H,如图:
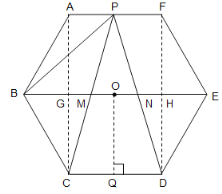
∵六边形ABCDEF是正六边形,P是AF的中点
∴∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=∠BAF=120°,AB=BC=CD=DE=EF=AF,BE平分∠ABC,EB平分∠DEF,AP=PF
∴∠BAC=∠BCA=![]() =30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG
=30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG
∴AB=2BG,∠CAF=∠AFD=∠CDF=∠GCD=∠OGC=90°
∴四边形ACDF和四边形OGCQ都是矩形
∴AF∥GH∥CD,AF=GH=CD,OQ=CG=AG
设BG=a,则AB=2a
∴AP=![]() AF=
AF=![]() AB=
AB=![]() ×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a
×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a
∵GM∥AP
∴△CGM∽△CAP
∴![]()
∴GM=![]() AP=
AP=![]() a
a
同理可得NH=![]() PF=
PF=![]() a,
a,
∴BM=BG+GM=a+![]() a=
a=![]() a,MN=GH-GM-NH=2a-
a,MN=GH-GM-NH=2a-![]() a-
a-![]() a=a
a=a
在Rt△ABG中,AG=![]()
∴OQ=GC=AG=![]()
∴![]() =
=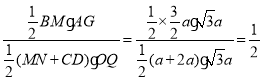
故选A.

 阅读快车系列答案
阅读快车系列答案