Question

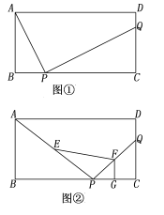
【题目】在矩形ABCD中，AB＝5cm，BC＝10cm，点P从点A出发，沿AB边向点B以每秒1cm的速度移动，同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动，P、Q两点在分别到达B、C两点时就停止移动，设两点移动的时间为t秒，解答下列问题：

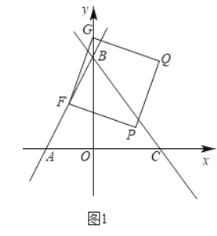
（1）如图1，当t为几秒时，△PBQ的面积等于4cm2？

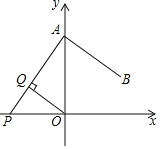
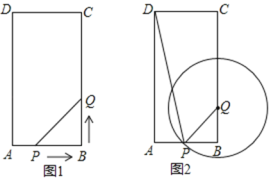
（2）如图2，以Q为圆心，PQ为半径作⊙Q．在运动过程中，是否存在这样的t值，使⊙Q正好与四边形DPQC的一边（或边所在的直线）相切？若存在，求出t值；若不存在，请说明理由．

Answer 1

【答案】（1）t=1秒或4秒；（2）t＝0秒或(﹣15+)秒.

【解析】

（1）由题意可知PA＝t，BQ＝2t，从而得到PB＝5﹣t，BQ＝2t，然后根据△PQB的面积＝4cm2列方程求解即可；

（2）当t＝0时，点P与点A重合时，点B与点Q重合，此时圆Q与PD相切；当⊙Q正好与四边形DPQC的DC边相切时，由圆的性质可知QC＝QP，然后依据勾股定理列方程求解即可；

解：（1）∵当运动时间为t秒时，PA＝t，BQ＝2t，

∴PB＝5﹣t，BQ＝2t．

∵△PBQ的面积等于4cm2，

∴PBBQ＝（5﹣t）2t．

∴（5﹣t）2t＝4．

解得：t1＝1，t2＝4．

答：当t为1秒或4秒时，△PBQ的面积等于4cm2；

（2）由题意可知圆Q与PQ、CQ不相切．下面分两种情况讨论：

（Ⅰ）如图1所示：当t＝0时，点P与点A重合时，点B与点Q重合．

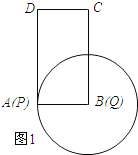
∵∠DAB＝90°，

∴∠DPQ＝90°．

∴DP⊥PQ．

∴DP为圆Q的切线．

（Ⅱ）当⊙Q正好与四边形DPQC的DC边相切时，如图2所示．

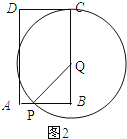
由题意可知：PB＝5﹣t，BQ＝2t，PQ＝CQ＝10﹣2t．

在Rt△PQB中，由勾股定理可知：PQ2＝PB2+QB2，即（5﹣t）2+（2t）2＝（10﹣2t）2．

解得：t1＝﹣15+，t2＝﹣15﹣（舍去）．

综上所述可知当t＝0秒或t＝(﹣15+)秒时，⊙Q与四边形DPQC的一边相切．