��Ŀ����
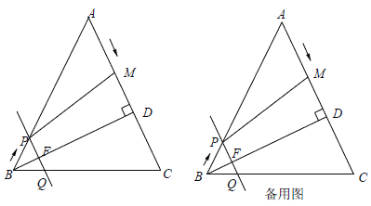
����Ŀ������ABC�У�AC��BC����ACB��90������P����ƽ���ڲ����A��B��C�غϵ�����һ�㣬����PC�����߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC������AD��BP��
��1���۲����
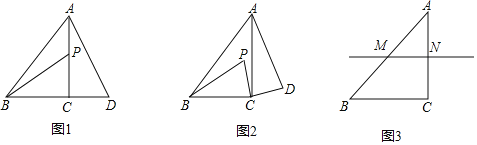
����P��ֱ��AC��ʱ����ͼ1���߶�BP��AD��������ϵ���� ����ֱ��BP��ֱ��AD��λ�ù�ϵ���� ����
��2����չ̽��
����P����ֱ��AC��ʱ����1���е�������ϵ��λ�ù�ϵ�������𣿲���ͼ2������˵�����ɣ�
��3���������
����M��N�ֱ���AB��AC���е㣬��P��ֱ��MN�ϣ���ֱ��д����A��P��D��ͬһ��ֱ����ʱ![]() ��ֵ��
��ֵ��
���𰸡���1��BP��AD��BP��AD����2�����������ɼ���������3��![]() ��
�� ![]()
��������
��1���۲����,��ͼ1���ӳ�BP��AD��H������SAS����֤��ACD�ա�BCP���ɵ�BP=AD����CAD=��CBP������ǵ����ʿ�֤BP��AD��
��2����չ̽��,��ͼ2���ӳ�BP��AD��H������SAS����֤��ACD�ա�BCP���ɵ�BP=AD����CAD=��CBP�����������ڽǺͶ�����֤BP��AD��
��3���������,������������ۣ�����SAS����֤��ACD�ա�BCP���ɵ�BP=AD�����߶δ�ֱƽ���ߵ����ʿɵ�AP=PC��������⣮
�⣺��1���۲����
��ͼ1���ӳ�BP��AD��H��

�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90����
���ACB����PCD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��BP��AD����CAD����CBP��
�ߡ�CAD+��D��90����
���CBP+��D��90����
���BHD��90����
��BP��AD��
�ʴ�Ϊ��BP��AD��BP��AD��
��2����չ̽��
��Ȼ������
�������£���ͼ2���ӳ�BP��AD��H��
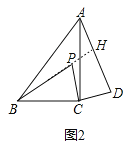
�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90������ACB��
���BCP����ACD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��BP��AD����CAD����CBP��
�ߡ�CBP+��ABP+��BAC��90����
���CAD+��ABP+��BAC��90����
���AHB��90����
��BP��AD��
��3���������
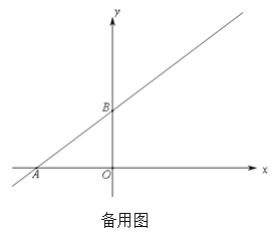
����A���߶�PD��ʱ����ͼ3������BP��
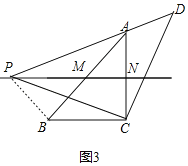
�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90������ACB��
���BCP����ACD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��PB��AD��
�ߵ�M��N�ֱ���AB��AC���е㣬
��MN��BC��
���ANM����ACB��90������AN��CN��
��PN��AC���д��ߣ�
��AP��PC��
��PC��CD����PCD��90��
��PD��![]() PC��
PC��
��AD��PD��AP��![]() PC��PC��BP��
PC��PC��BP��
��![]() ��
��
����P���߶�AD��ʱ����ͼ4������BP��

�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90������ACB��
���BCP����ACD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��PB��AD��
�ߵ�M��N�ֱ���AB��AC���е㣬
��MN��BC��
���ANM����ACB��90������AN��CN��
��PN��AC���д��ߣ�
��AP��PC��
��PC��CD����PCD��90��
��PD��![]() PC��
PC��
��AD��PD+AP��![]() PC+PC��BP��
PC+PC��BP��
��![]() ��
��