题目内容
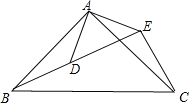
【题目】如图,DB=DC,∠BAC=∠BDC=120°,DM⊥AC,E为BA延长线上的点,∠BAC的角平分线交BC于N,∠ABC的外角平分线交CA的延长线于点P,连接PN交AB于K,连接CK,则下列结论正确的是:①∠ABD=∠ACD;②DA平分∠EAC;③当点A在DB左侧运动时,![]() 为定值;④∠CKN=30° ( )
为定值;④∠CKN=30° ( )
A.①③④B.②③④C.①②④D.①②③
【答案】C
【解析】
由∠BAC=∠BDC=120°可知ABCD四点共圆,由圆周角定理可得∠ABD=∠ACD,∠DAC=∠DBC=30°,即可得到∠DAC=∠EAD=30°,所以①②正确;无法得出③的结论,故③错误;PKN截△ABC,根据梅涅劳斯定理可得![]() ,再根据角平分线定理可推出
,再根据角平分线定理可推出![]() ,
,![]() ,从而得出
,从而得出![]() ,可知CK为∠ACB的角平分线,两条角平分线交点为△ABC的内心G,设△ANC的内心为H,易知H在CG上,连接AH,NH,可得角平分线,最后推出AKNH四点共圆,即可得∠CKN=∠NAH=30°,故④正确.
,可知CK为∠ACB的角平分线,两条角平分线交点为△ABC的内心G,设△ANC的内心为H,易知H在CG上,连接AH,NH,可得角平分线,最后推出AKNH四点共圆,即可得∠CKN=∠NAH=30°,故④正确.
解:∵∠BAC=∠BDC=120°
∴ABCD四点共圆,∠DBC=∠DCB=30°,如图所示,
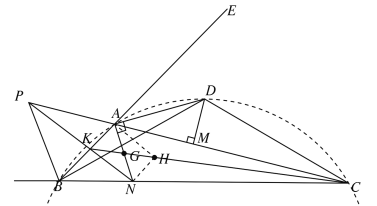
∴∠ABD=∠ACD,∠DAC=∠DBC=30°,
故①正确;
又∵∠EAC=180°-∠BAC=60°,
∴∠EAD=∠EAC-∠DAC=30°=∠AEC
即AD平分∠EAC,故②正确;
无法得出③的结论,故③错误;
④PKN截△ABC,根据梅涅劳斯定理可得![]() ,
,
∵AN平分∠BAC,PB平分△ABC的外角,
∴![]() ,
,![]()
∴![]() ,整理得
,整理得![]()
∴CK平分∠ACB
AN,CK交于点G,则G为△ABC的内心,
设△ANC的内心为H,易知H在CG上,
连接AH,NH,则AH平分∠NAC,NH平分∠ANC
设∠ACB=![]() ,则∠ABC=
,则∠ABC=![]() ,
,
∴∠ANC=∠ABC+∠BAN=![]()
∴∠ANH=![]() ∠ANC=
∠ANC=![]()
又∵∠AKG=∠ABC+∠KCB=![]()
∴∠ANH=∠AKG
∴AKNH四点共圆,
∴∠CKN=∠NAH=30°,故④正确.
①②④正确,故选C.

 习题精选系列答案
习题精选系列答案【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.