题目内容
【题目】如图,在△ABC与△ADE中,∠BAC=∠DAE=90°,AD=AE,AB=AC,且B、D、E三点在一条直线上.
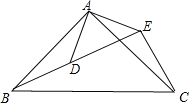
(1)求证:BD=CE.
(2)求∠BEC的度数.
(3)写出BE与AE、CE的数量关系是 .
【答案】(1)见解析;(2)∠BEC=90°;(3)结论:BE=CE+![]() AE.理由见解析.
AE.理由见解析.
【解析】
(1)欲证明BD=CE,只要证明△ABD≌△ACE即可;
(2)利用全等三角形的性质可得∠AEC=∠ADB=135°,即可解决问题;
(3)结论:BE=EC+![]() AE.利用全等三角形的性质以及等腰直角三角形的性质即可证明.
AE.利用全等三角形的性质以及等腰直角三角形的性质即可证明.
(1)证明:∠BAC=∠DAE=90°
∴∠BAD=∠CAE,
∵AB=AC,AD=AE
∴△ABD≌△ACE,
∴BD=CE.
(2)解:∵△ABD≌△ACE,
∴∠ADB=∠AEC,
又∵∠ADB=∠DAE+∠AED=135°,
∴∠AEC=∠AED+∠BEC=135°,
∴135°=45°+∠BEC
∴∠BEC=90°.
③解:结论:BE=CE+![]() AE.
AE.
理由:∵△ABD≌△ACE,
∴BD=CE,
∵△ADE是等腰直角三角形,
∴DE=![]() AE,
AE,
∴BE=BD+DE=CE+![]() AE.
AE.

练习册系列答案
相关题目