题目内容
【题目】顺次连接边长为![]() 的正六边形的不相邻的三边的中点,又形成一个新的正三角形,则这个新的正三角形的面积等于( )
的正六边形的不相邻的三边的中点,又形成一个新的正三角形,则这个新的正三角形的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
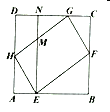
作AP⊥GH于P,BQ⊥GH于Q,由正六边形和等边三角形的性质求出GH=PG+PQ+QH=9cm,由等边三角形的面积公式即可得出答案.
如图所示:作AP⊥GH于P,BQ⊥GH于Q,如图所示:

∵△GHM是等边三角形,
∴∠MGH=∠GHM=60°,
∵六边形ABCDEF是正六边形,
∴∠BAF=∠ABC=120°,正六边形ABCDEF是轴对称图形,
∵G、H、M分别为AF、BC、DE的中点,△GHM是等边三角形,
∴AG=BH=3cm,∠MGH=∠GHM=60°,∠AGH=∠FGM=60°,
∴∠BAF+∠AGH=180°,
∴AB∥GH,
∵作AP⊥GH于P,BQ⊥GH于Q,
∴PQ=AB=6cm,∠PAG=90°-60°=30°,
∴PG=![]() AG=
AG=![]() cm,
cm,
同理:QH=![]() cm,
cm,
∴GH=PG+PQ+QH=9cm,
∴△GHM的面积=![]() GH2=
GH2=![]() cm2;
cm2;
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目