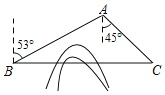
题目内容
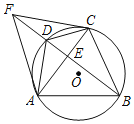
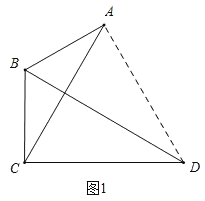
【题目】在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.
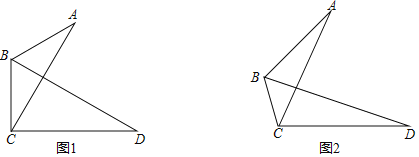
(1)如图1,若AB=BC,求证:BD平分∠ABC;
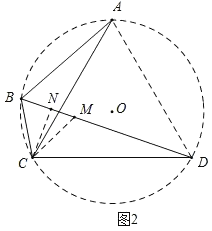
(2)如图2,若AB=2BC,
①求![]() 的值;
的值;
②连接AD,当S△ABC=![]() 时,直接写出四边形ABCD的面积为 .
时,直接写出四边形ABCD的面积为 .
【答案】(1)详见解析;(2)① ![]() ;②
;② ![]() .
.
【解析】
(1)连接AD,证△ACD是等边三角形,再证△ABD≌△CBD,推出∠CBD=∠ABD,即得出结论;
(2)①连接AD,作等边三角形ACD的外接圆⊙O,证点B在⊙O上,在BD上截取BM,使BM=BC,证△CBA≌△CMD,设BC=BM=1,则AB=MD=2,BD=3,过点C作CN⊥BD于N,可求出BN=![]() BC=
BC=![]() ,CN=
,CN=![]() BC=
BC=![]() ,ND=BD﹣BN=
,ND=BD﹣BN=![]() ,CD=
,CD=![]() ,即可求出
,即可求出![]() =
=![]() =
=![]() ;
;
②分别过点B,D作AC的垂线,垂足分别为H,Q,设CB=1,AB=2,CH=x,则由①知,AC=![]() ,AH=
,AH=![]() ﹣x,在Rt△BCH与Rt△BAH中利用勾股定理求出BH的值,再求出DQ的值,求出
﹣x,在Rt△BCH与Rt△BAH中利用勾股定理求出BH的值,再求出DQ的值,求出![]() =
=![]() ,因为AC为△ABC与△ACD的公共底,所以
,因为AC为△ABC与△ACD的公共底,所以![]() =
=![]() ,可求出△ACD的面积,进一步求出四边形ABCD的面积.
,可求出△ACD的面积,进一步求出四边形ABCD的面积.
(1)证明:如图1,连接AD,
由题意知,∠ACD=60°,CA=CD,
∴△ACD是等边三角形,
∴CD=AD,
又∵AB=CB,BD=BD,
∴△ABD≌△CBD(SSS),
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)解:①如图2,连接AD,作等边三角形ACD的外接圆⊙O,
∵∠ADC=60°,∠ABC=120°,
∴∠ADC+∠ABC=180°,
∴点B在⊙O上,
∵AD=CD,
∴![]() ,
,
∴∠CBD=∠CAD=60°,
在BD上截取BM,使BM=BC,
则△BCM为等边三角形,
∴∠CMB=60°,
∴∠CMD=120°=∠CBA,
又∵CB=CM,∠BAC=∠BDC,
∴△CBA≌△CMD(AAS),
∴MD=AB,
设BC=BM=1,则AB=MD=2,
∴BD=3,
过点C作CN⊥BD于N,
在Rt△BCN中,∠CBN=60°,
∴∠BCN=30°,
∴BN=![]() BC=
BC=![]() ,CN=
,CN=![]() BC=
BC=![]() ,
,
∴ND=BD﹣BN=![]() ,
,
在Rt△CND中,
CD=![]() =
=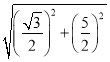 =
=![]() ,
,
∴AC=![]() ,
,
∴![]() =
=![]() ;
;
②如图3,分别过点B,D作AC的垂线,垂足分别为H,Q,
设CB=1,AB=2,CH=x,
则由①知,AC=![]() ,AH=
,AH=![]() -x,
-x,
在Rt△BCH与Rt△BAH中,
BC2﹣CH2=AB2﹣AH2,
即1﹣x2=22-(![]() -x)2,
-x)2,
解得,x=![]() ,
,
∴BH=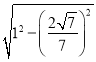 =
=![]() ,
,
在Rt△ADQ中,DQ=![]() AD=
AD=![]() ×
×![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∵AC为△ABC与△ACD的公共底,
∴![]() =
=![]() =
=![]() ,
,
∵S△ABC=![]() ,
,
∴S△ACD=![]() ,
,
∴S四边形ABCD=![]() =
=![]() ,
,
故答案为:![]() .
.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案