题目内容
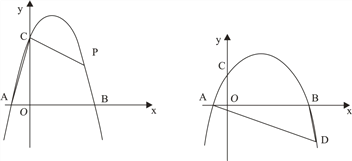
【题目】抛物线![]() 与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
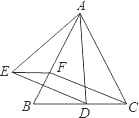
(1)如图1,若A(-1,0),B(3,0),
① 求抛物线![]() 的解析式;
的解析式;
② P为抛物线上一点,连接AC,PC,若∠PCO=3∠ACO,求点P的横坐标;
(2)如图2,D为x轴下方抛物线上一点,连DA,DB,若∠BDA+2∠BAD=90°,求点D的纵坐标.
![]()
【答案】(1)①y=-x2+2x+3②![]() (2)-1
(2)-1
【解析】(1)①把A、B的坐标代入解析式,解方程组即可得到结论;
②延长CP交x轴于点E,在x轴上取点D使CD=CA,作EN⊥CD交CD的延长线于N.由CD=CA ,OC⊥AD,得到∠DCO=∠ACO.由∠PCO=3∠ACO,得到∠ACD=∠ECD,从而有tan∠ACD=tan∠ECD,
![]() ,即可得出AI、CI的长,进而得到
,即可得出AI、CI的长,进而得到![]() .设EN=3x,则CN=4x,由tan∠CDO=tan∠EDN,得到
.设EN=3x,则CN=4x,由tan∠CDO=tan∠EDN,得到![]() ,故设DN=x,则CD=CN-DN=3x=
,故设DN=x,则CD=CN-DN=3x=![]() ,解方程即可得出E的坐标,进而求出CE的直线解析式,联立解方程组即可得到结论;
,解方程即可得出E的坐标,进而求出CE的直线解析式,联立解方程组即可得到结论;
(2)作DI⊥x轴,垂足为I.可以证明△EBD∽△DBC,由相似三角形对应边成比例得到![]() ,
,
即![]() ,整理得
,整理得![]() .令y=0,得:
.令y=0,得:![]() .
.
故![]() ,从而得到
,从而得到![]() .由
.由![]() ,得到
,得到![]() ,解方程即可得到结论.
,解方程即可得到结论.
(1)①把A(-1,0),B(3,0)代入![]() 得:
得:
![]() ,解得:
,解得:![]() ,
,
∴![]()
②延长CP交x轴于点E,在x轴上取点D使CD=CA,作EN⊥CD交CD的延长线于N.
∵CD=CA ,OC⊥AD,∴ ∠DCO=∠ACO.
∵∠PCO=3∠ACO,∴∠ACD=∠ECD,∴tan∠ACD=tan∠ECD,
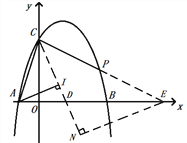
∴![]() ,AI=
,AI=![]() ,
,
∴CI=![]() ,∴
,∴![]() .
.
设EN=3x,则CN=4x.
∵tan∠CDO=tan∠EDN,
∴![]() ,∴DN=x,∴CD=CN-DN=3x=
,∴DN=x,∴CD=CN-DN=3x=![]() ,
,
∴![]() ,∴DE=
,∴DE=![]() ,E(
,E(![]() ,0).
,0).
CE的直线解析式为:![]() ,
,
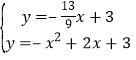
![]() ,解得:
,解得:![]() .
.
点P的横坐标![]() .
.
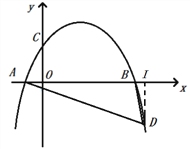
(2)作DI⊥x轴,垂足为I.
∵∠BDA+2∠BAD=90°,∴∠DBI+∠BAD=90°.
∵∠BDI+∠DBI=90°,∴∠BAD=∠BDI.
∵∠BID=∠DIA,∴△EBD∽△DBC,∴![]() ,
,
∴![]() ,
,
∴![]() .
.
令y=0,得:![]() .
.
∴![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
解得:yD=0或-1.
∵D为x轴下方一点,
∴![]() ,
,
∴D的纵坐标-1 .

【题目】某超市对![]() ,
,![]() 两种商品开展春节促销活动,活动方案有如下两种:
两种商品开展春节促销活动,活动方案有如下两种:
商品 |
|
| |
标价(单位:元) | 120 | 150 | |
方案一 | 每件商品出售价格 | 按标价打7折 | 按标价打 |
方案二 | 若所购商品超过10件(不同商品可累计)时,每件商品均按标价打8折后出售. | ||
(同一种商品不可同时参与两种活动)
(1)某单位购买![]() 商品5件,
商品5件,![]() 商品4件,共花费960元,求
商品4件,共花费960元,求![]() 的值;
的值;
(2)在(1)的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.
商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.