题目内容
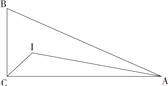
【题目】如图，
中，
，
，
.
（1）试用直尺和圆规，在直线AB上求作点P，使
为等腰三角形．要求：①保留作图痕迹；②若点P有多解，则应作出所有的点P，并在图中依次标注
、
、
…；
（2）根据（1）求PA的长（所有可能的值）.
【答案】（1）如图；见解析；（2）
，
，
，
.
【解析】
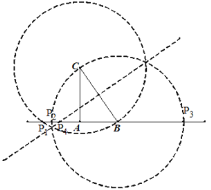
（1）以C点为圆心，CB为半径画弧交AB于P1，以B点为圆心，BC为半径画弧交直线AB于P2、P3，作BC的垂直平分线交直线AB于P4；（2）利用等腰三角形性质和勾股定理，即可求出.
（1）如图，点P1、P2、P3、P4为所作；
（2）解：∵
为直角三角形，
① 当CP1=CB时
∵CA⊥BP1
∴AP1=AB=3
②当BP2=BP3=BA=5时
AP2=AB+BP2=3+5=8
③AP3=BP3-AB=2；
④当P4C=P4B时，
设AP4=x，则P4C=P4B=x+3；
由勾股定理得：
解得：
即
综上所述，AP的值可能为2、3、8、
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
