题目内容
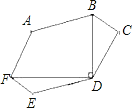
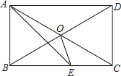
【题目】如图,在⊙O 中,BC是弦,OA⊥BC于点E,D为⊙O上一点,连接AD,CD.
(1)求证:∠AOB=2∠ADC;
(2)若OB⊥CD,CD=8,OE=![]() ,求tan∠ADC.
,求tan∠ADC.
【答案】(1)证明见解析(2)![]()
【解析】(1)连接OC.由垂径定理得∠AOC=∠AOB.再由圆周角定理即可得到结论;
(2)延长BO交CD于点F,连接AB.由垂径定理得到CF的长.由∠EBO=∠FBC,∠CFB=∠OEB,得到 △ABE∽△DFC,由相似三角形对应边成比例得到![]() .设BE=
.设BE=![]() ,则BF=4n,BC=
,则BF=4n,BC=![]() ,由勾股定理得CF=
,由勾股定理得CF=![]() ,由2n=4,得到n,BE,
,由2n=4,得到n,BE,
BO,AE的长,由tan∠ADC=tan∠ABE即可得到结论.
(1)连接OC.

∵OA⊥BC,∴弧AC=弧AB,∴∠AOC=∠AOB.
∵∠AOC=2∠ADC,∴∠AOB=2∠ADC .
(2)延长BO交CD于点F,连接AB.
∵OB⊥CD,∴CF=![]() CD=4.
CD=4.
∵∠EBO=∠FBC,∠CFB=∠OEB,
∴ △ABE∽△DFC,∴![]() .
.
设BE=![]() ,则BF=4n,BC=
,则BF=4n,BC=![]() ,
,
∴CF=![]() ,∴2n=4,n=2,∴BE=
,∴2n=4,n=2,∴BE=![]() =
=![]() ,
,
∴BO=5,AE=![]() ,∴tan∠ADC=tan∠ABE=
,∴tan∠ADC=tan∠ABE=![]() .
.

【题目】如图1是边长为![]() 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
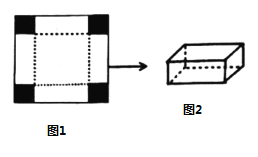
(1)设剪去的小正方形的边长为![]() ,折成的长方体盒子的容积为
,折成的长方体盒子的容积为![]() ,直接写出用只含字母
,直接写出用只含字母![]() 的式子表示这个盒子的高为______
的式子表示这个盒子的高为______![]() ,底面积为______
,底面积为______![]() ,盒子的容积
,盒子的容积![]() 为______
为______![]() ,
,
(2)为探究盒子的体积与剪去的小正方形的边长![]() 之间的关系,小明列表
之间的关系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 324 |
| 588 | 576 | 500 |
| 252 | 128 |
填空:①![]() ______,
______,![]() ______;
______;
②由表格中的数据观察可知当![]() 的值逐渐增大时,
的值逐渐增大时,![]() 的值______.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)
的值______.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)