题目内容
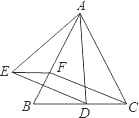
【题目】如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB=60°，DC=EF．
（1）求证：四边形EFCD是平行四边形；
（2）若BF=EF，求证：AE=AD．
【答案】
【1】（1）证明：△ABC是等边三角形
∴∠B=60
∵∠EFB=60，∴∠B=∠EFB，∴EF∥DC……………………2分
∵DC=EF，∴四边形EFCD是平行四边形…………4分
【2】（2）连接BE
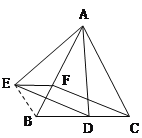
∵BF=EF，∠EFB=60
∴△EFB是等边三角形，∴EB=EF，∠EBF=60………………6分
∵DC=EF，∴EB=DC
∵△ABC是等边三角形，∴∠ACB=60，AB=AC
∴∠EBF=∠ACB………………8分
∴△AEB≌△ADC，∴AE=AD………………10分
【解析】试题分析：（1）由△ABC是等边三角形得到∠B=60°，而∠EFB=60°，由此可以证明EF∥DC，而DC=EF，然后即可证明四边形EFCD是平行四边形；
（2）如图，连接BE，由BF=EF，∠EFB=60°可以推出△EFB是等边三角形，然后得到EB=EF，∠EBF=60°，而DC=EF，由此得到EB=DC，又
△ABC是等边三角形，所以得到∠ACB=60°，AB=AC，然后即可证明△AEB≌△ADC，利用全等三角形的性质就证明AE=AD．
试题解析：（1）∵△ABC是等边三角形，
∴∠ABC=60°，
∵∠EFB=60°，
∴∠ABC=∠EFB，
∴EF∥DC（内错角相等，两直线平行），
∵DC=EF，
∴四边形EFCD是平行四边形；
（2）连接BE
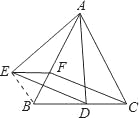
∵BF=EF，∠EFB=60°，
∴△EFB是等边三角形，
∴EB=EF，∠EBF=60°
∵DC=EF，
∴EB=DC，
∵△ABC是等边三角形，
∴∠ACB=60°，AB=AC，
∴∠EBF=∠ACB，
∴△AEB≌△ADC，
∴AE=AD．
