题目内容
【题目】如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)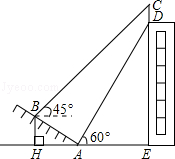
(1)求点B距水平而AE的高度BH;
(2)求宣传牌CD的高度.
(结果精确到0.1米.参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
【答案】
(1)
解:在Rt△ABH中,
∵tan∠BAH= ![]() =i=
=i= ![]() =
= ![]() .
.
∴∠BAH=30°,
∴BH=AB.sin∠BAH=10.sin30°=10× ![]() =5.
=5.
答:点B距水平面AE的高度BH是5米;
(2)
解:在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5 ![]() ,
,
在Rt△ADE中,tan∠DAE= ![]() ,
,
即tan60°= ![]() ,∴DE=15
,∴DE=15 ![]() ,
,
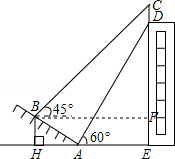
如图,过点B作BF⊥CE,垂足为F,
∴BF=AH+AE=5 ![]() +15,
+15,
DF=DE﹣EF=DE﹣BH=15 ![]() ﹣5,
﹣5,
在Rt△BCF中,∠C=90°﹣∠CBF=90°﹣45°=45°,
∴∠C=∠CBF=45°,
∴CF=BF=5 ![]() +15,
+15,
∴CD=CF﹣DF=5 ![]() +15﹣(15
+15﹣(15 ![]() ﹣5)=20﹣10
﹣5)=20﹣10 ![]() ≈20﹣10×1.732≈2.7(米),
≈20﹣10×1.732≈2.7(米),
答:广告牌CD的高度约为2.7米.
【解析】(1)在Rt△ABH中,由tan∠BAH= ![]() =i=
=i= ![]() =
= ![]() .得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×
.得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10× ![]() =5;(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5
=5;(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5 ![]() ,在Rt△ADE中,tan∠DAE=
,在Rt△ADE中,tan∠DAE= ![]() ,即tan60°=
,即tan60°= ![]() ,得到DE=15
,得到DE=15 ![]() ,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5
,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5 ![]() +15,于是得到DF=DE﹣EF=DE﹣BH=15
+15,于是得到DF=DE﹣EF=DE﹣BH=15 ![]() ﹣5,在Rt△BCF中,∠C=90°﹣∠CBF=90°﹣45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5
﹣5,在Rt△BCF中,∠C=90°﹣∠CBF=90°﹣45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5 ![]() +15,即可求得结果.
+15,即可求得结果.
【考点精析】关于本题考查的关于仰角俯角问题,需要了解仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
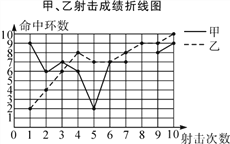
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?