题目内容
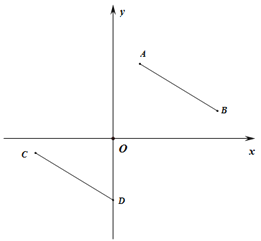
【题目】已知,在平面直角坐标系中,A(1,a)、B(b,1),其中a、b满足![]() +(a+b-7)2=0.
+(a+b-7)2=0.
(1) 求a、b的值;
(2) 平移线段AB至CD,其中A、B的对应点分别为C、D,若D的坐标为(0,n)且n<0,若四边形ABDC的面积为20,求D的坐标;
(3)在(2)的条件下,将线段AB绕点A以每秒80的速度顺时针旋转,同时线段CD绕点D以每秒20的速度顺时针旋转(当AB旋转到一周时两线段同时停止旋转),设运动时间为t秒,当t为何值时,直线AB与直线CD的夹角为600?请说明理由.
【答案】(1)![]() ;(2)D(0,
;(2)D(0,![]() );(3)当t为10秒,20秒或40秒时,直线AB与直线CD的夹角为60°.
);(3)当t为10秒,20秒或40秒时,直线AB与直线CD的夹角为60°.
【解析】
(1)由a、b满足![]() +(a+b-7)2=0可得:2a-b-2=0,a+b-7=0,由这两个等式组成关于a、b的方程组,解此方程组即可求得a、b的值;
+(a+b-7)2=0可得:2a-b-2=0,a+b-7=0,由这两个等式组成关于a、b的方程组,解此方程组即可求得a、b的值;
(2)如下图,分别过点A,B作AE⊥y轴E, BF⊥y轴F,由S平行四边形ABDC=20可得S△ABD= S四边形AEFB+S△BFD- S△AFD=10,因此结合图形和题意列出关于n的方程,解方程求得n的值即可得到点D的坐标;
(3)设旋转后直线AB′与DC′交于点E,过点E作直线EF∥AB,则可得: EF∥AB∥CD,然后分∠AEC′=60°,∠AED=60°,∠B′EC′=60°三种情况结合图1、图2和图3及已知条件进行分析解答即可.
(1)∵a、b满足![]() +(a+b-7)2=0,
+(a+b-7)2=0,
∴![]() ,解得:
,解得:![]() ;
;
(2)分别过点A,B作AE⊥y轴E, BF⊥y轴F,
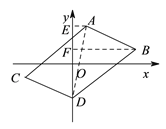
∵S平行四边形ABDC=20,
S△ABD= S四边形AEFB+S△BFD- S△AFD,
又∵A(1,3),B(4,1),D(0,n),
∴S△ABD=![]() =10, 解得
=10, 解得![]()
∴点 D的坐标为(0,![]() );
);
(3)设旋转后直线AB′与DC′交于点E,过点E作直线EF∥AB,
∵AB∥CD,
∴ EF∥AB∥CD.
①如图1,若∠AEC′=60°,
∵EF∥AB∥CD,
∴∠AEF=∠BAB′=8t,∠FEC′=∠CDC′=2t,
∴∠AEC′=8t-2t=60°,解得t=10;

②如图2,若∠AED=60°,
∵EF∥AB∥CD,
∴∠AEF+∠BAB′=180°,∠FED=∠CDC′=2t,
∴∠AEF=180°-8t,
∵∠AED=∠AEF+∠FED=60°,
∴180°-8t+2t=60°,解得:t=20;
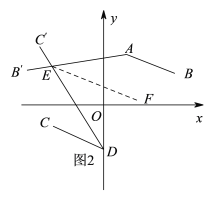
③如图3,若∠B′EC′=60°,
∵EF∥AB∥CD,
∴∠FEB′=∠BAB′=360°-8t,∠FED=∠CDC′=2t,
∵∠B′EC′=180°-∠FEB′-∠FED=60°,
∴180°-(360-8t)-2t=60°,解得:t=40;

综上所述,当t为10秒,20秒或40秒时,直线AB与直线CD的夹角为60°.

【题目】甲、乙两台机床同时生产一种零件,在10天中,两台机床每天出次品的数量如下表:
甲 | 1 | 1 | 0 | 2 | 1 | 3 | 2 | 1 | 1 | 0 |
乙 | 0 | 2 | 2 | 0 | 3 | 1 | 0 | 1 | 3 | 1 |
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果来看,在10天中,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?