题目内容
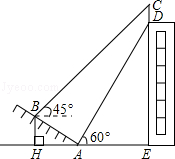
【题目】如图,在△ABC中,AB=7,AC=![]() ,∠A=45°,AH⊥HC,垂足为H。
,∠A=45°,AH⊥HC,垂足为H。
(1)求证:△AHC是等腰直角三角形;
(2)求BC的长.

【答案】(1)见解析;(2)BC=5
【解析】试题分析:(1)先证得∠AHC=90°,再由∠A=45°,即可证得△AHC是等腰直角三角形;(2)设AH=x,则CH=x,BH=7-x,在等腰直角三角形△AHC中,根据勾股定理求得CH=4,即可得BH=3,在Rt△BHC中,根据勾股定理求得BC=5.
试题解析:
(1)证明:∵AH⊥HC,
∴∠AHC=∠BHC=90°,
∵∠A=45°,
∴∠ACH=45°,
∴△AHC是等腰直角三角形;
(2)设AH=x,则CH=x,BH=7-x,
在等腰直角三角形△AHC中,
![]() ,
,
![]()
解得x=4.
∴CH=3,BH=4,
在Rt△BHC中,
![]() ,
,
∴BC=5.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目