题目内容
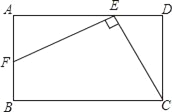
【题目】矩形ABCD中,E在AD上,F在AB上,EF⊥CE于E,DE=AF=2,矩形的周长为24,则BF的长为( )
A. 3 B. 4 C. 5 D. 7
【答案】A
【解析】
先根据直角三角形的性质证明得到∠AEF=∠DCE,然后利用“角角边”证明△AEF和△DCE全等,根据全等三角形对应边相等可得AE=DC,再利用矩形的周长求出CD的长度,根据BF=AB-AF,代入数据计算即可得解.
∵EF⊥CE,
∴∠AEF+∠DEC=90°,
在矩形ABCD中,∠D=90°,
∴∠DCE+∠DEC=90°,
∴∠AEF=∠DCE,
在△AEF和△DCE中,
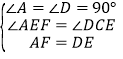 ,
,
∴△AEF≌△DCE(AAS),
∴AE=DC,
∵矩形的周长为24,
∴2(AE+DE+DC)=24,
即2(DC+2+DC)=24,
解得DC=5,
∴BF=ABAF=52=3.
故选A.

练习册系列答案
相关题目