Question

【题目】类比等腰三角形的定义，我们定义：有三条边相等的凸四边形叫做“准等边四边形”．

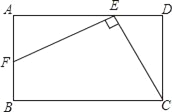
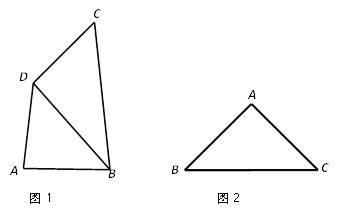
（1）已知：如图1，在“准等边四边形”ABCD中，BC≠AB，BD⊥CD，AB=3，BD=4，求BC的长；

（2）在探究性质时，小明发现一个结论：对角线互相垂直的“准等边四边形”是菱形．请你判断此结论是否正确，若正确，请说明理由；若不正确，请举出反例；

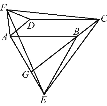
（3）如图2，在△ABC中，AB=AC=，∠BAC=90°．在AB的垂直平分线上是否存在点P，使得以A，B，C，P为顶点的四边形为“准等边四边形”． 若存在，请求出该“准等边四边形”的面积；若不存在，请说明理由．

Answer 1

【答案】（1）5；（2）正确，证明详见解析；（3）存在，有四种情况，面积分别是：，，，

【解析】

（1）根据勾股定理计算BC的长度,

（2）根据对角线互相垂直平分的四边形是菱形判断,

（3）有四种情况，作辅助线，将四边形分成两个三角形和一个四边形或两个三角形，相加可得结论.

（1）∵BD⊥CD

∴∠BDC=90°，BC>CD

∵在“准等边四边形”ABCD中，BC≠AB，

∴AB=AD=CD=3,

∵BD=4，

∴BC=,

（2）正确．

如图所示：

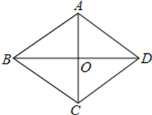
∵AB=AD

∴ΔABD是等腰三角形．

∵AC⊥BD．

∴AC垂直平分BD．

∴BC=CD

∴CD =AB=AD=BC

∴四边形 ABCD是菱形．

（3）存在四种情况，

如图2，四边形ABPC是“准等边四边形”,过C作于F，则,

∵EP是AB的垂直平分线，

∴ ,

∴四边形AEFC是矩形，

在中， ,

∴ ,

∵

∴

∴

如图4，四边形ABPC是“准等边四边形”,

∵ ,

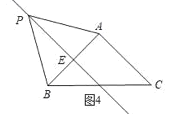
∴是等边三角形，

∴ ;

如图5，四边形ABPC是“准等边四边形”,

∵ ,PE是AB的垂直平分线，

∴ E是AB的中点，

∴ ,

∴

∴

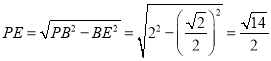
如图6，四边形ABPC是“准等边四边形”,过P作于F，连接AP，

∵，

∴，

∴