题目内容
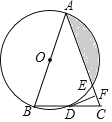
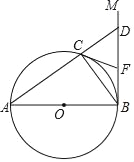
【题目】如图,AB为⊙O的直径,直线BM⊥AB于点B,点C在⊙O上,分别连接BC,AC,且AC的延长线交BM于点D,CF为⊙O的切线交BM于点F.
(1)求证:CF=DF;
(2)连接OF,若AB=10,BC=6,求线段OF的长.
【答案】(1)详见解析;(2)OF=![]() .
.
【解析】
(1)连接OC,如图,根据切线的性质得∠1+∠3=90°,则可证明∠3=∠4,再根据圆周角定理得到∠ACB=90°,然后根据等角的余角相等得到∠BDC=∠5,从而根据等腰三角形的判定定理得到结论;
(2)根据勾股定理计算出AC=8,再证明△ABC∽△ABD,利用相似比得到AD=![]() ,然后证明OF为△ABD的中位线,从而根据三角形中位线性质求出OF的长.
,然后证明OF为△ABD的中位线,从而根据三角形中位线性质求出OF的长.
(1)证明:连接OC,如图,

∵CF为切线,
∴OC⊥CF,
∴∠1+∠3=90°,
∵BM⊥AB,
∴∠2+∠4=90°,
∵OC=OB,
∴∠1=∠2,
∴∠3=∠4,
∵AB为直径,
∴∠ACB=90°,
∴∠3+∠5=90°,∠4+∠BDC=90°,
∴∠BDC=∠5,
∴CF=DF;
(2)在Rt△ABC中,AC=![]() =8,
=8,
∵∠BAC=∠DAB,
∴△ABC∽△ABD,
∴![]() ,即
,即![]() ,
,
∴AD=![]() ,
,
∵∠3=∠4,
∴FC=FB,
而FC=FD,
∴FD=FB,
而BO=AO,
∴OF为△ABD的中位线,
∴OF=![]() AD=
AD=![]() .
.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某市现在有两种用电收费方法:
分时电表 | 普通电表 | |
峰时(8:00~21:00) | 谷时(21:00到次日8:00) | |
电价0.55元/千瓦·时 | 电价0.35元/千瓦·时 | 电价0.52元/千瓦·时 |
小明家所在的小区用的电表都换成了分时电表.
解决问题:
(1)小明家庭某月用电总量为![]() 千瓦·时(
千瓦·时(![]() 为常数);谷时用电
为常数);谷时用电![]() 千瓦·时,峰时用电
千瓦·时,峰时用电![]() 千瓦·时,分时计价时总价为
千瓦·时,分时计价时总价为![]() 元,普通计价时总价为
元,普通计价时总价为![]() 元,求
元,求![]() ,
,![]() 与用电量的函数关系式.
与用电量的函数关系式.
(2)小明家庭使用分时电表是不是一定比普通电表合算呢?
(3)下表是路皓家最近两个月用电的收据:
谷时用电(千瓦·时) | 峰时用电(千瓦·时) |
181 | 239 |
根据上表,请问用分时电表是否合算?