题目内容
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.

(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;
(3)若过A,D,C三点的圆的半径为 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.

(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;
(3)若过A,D,C三点的圆的半径为
 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.(1)略
(2)证明略
(3)理由略
解:(1)作出圆心O, …………………………………………………1分
以点O为圆心,OA长为半径作圆.…………………………………………1分
(2)证明:∵CD⊥AC,∴∠ACD="90°."
∴AD是⊙O的直径……………1分
连结OC,∵∠A=∠B=30°,
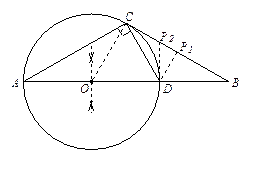
∴∠ACB=120°,又∵OA="OC,"
∴∠ACO=∠A =30°,…………1分
∴∠BCO=∠ACB-∠ACO ="120°-30°=90°. "
∴BC⊥OC,
∴BC是⊙O的切线. ……………………………………………1分
(3)存在. ……………………………………………………………………………1分
∵∠BCD=∠ACB-∠ACD=120°-90°=30°,
∴∠BCD=∠B, 即DB=DC.
又∵在Rt△ACD中,DC=AD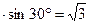 , ∴BD=
, ∴BD=  .
.
解法一:①过点D作DP1// OC,则△P1D B∽△COB,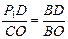 ,
,
∵BO=BD+OD=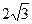 ,
,
∴P1D=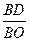 ×OC=
×OC=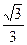 ×
×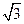 =
=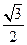 . ……………………………1分
. ……………………………1分
②过点D作DP2⊥AB,则△BDP2∽△BCO, ∴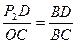 ,
,
∵BC=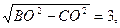
∴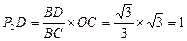 .………………………………………1分
.………………………………………1分
解法二:①当△B P1D∽△BCO时,∠DP1B=∠OCB=90°.
在Rt△B P1D中,
DP1=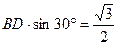 . ………………1分
. ………………1分
②当△B D P2∽△BCO时,∠P2DB=∠OCB=90°.
在Rt△B P2D中,
DP2=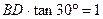 . ……………1分
. ……………1分
以点O为圆心,OA长为半径作圆.…………………………………………1分
(2)证明:∵CD⊥AC,∴∠ACD="90°."
∴AD是⊙O的直径……………1分
连结OC,∵∠A=∠B=30°,
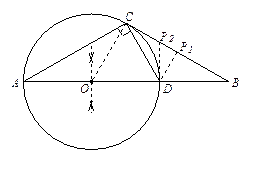
∴∠ACB=120°,又∵OA="OC,"
∴∠ACO=∠A =30°,…………1分
∴∠BCO=∠ACB-∠ACO ="120°-30°=90°. "
∴BC⊥OC,
∴BC是⊙O的切线. ……………………………………………1分
(3)存在. ……………………………………………………………………………1分
∵∠BCD=∠ACB-∠ACD=120°-90°=30°,
∴∠BCD=∠B, 即DB=DC.
又∵在Rt△ACD中,DC=AD
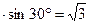 , ∴BD=
, ∴BD= 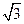 .
. 解法一:①过点D作DP1// OC,则△P1D B∽△COB,
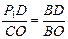 ,
,∵BO=BD+OD=
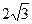 ,
,∴P1D=
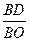 ×OC=
×OC=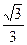 ×
×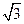 =
=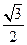 . ……………………………1分
. ……………………………1分②过点D作DP2⊥AB,则△BDP2∽△BCO, ∴
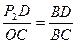 ,
,∵BC=
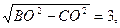
∴
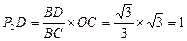 .………………………………………1分
.………………………………………1分解法二:①当△B P1D∽△BCO时,∠DP1B=∠OCB=90°.
在Rt△B P1D中,
DP1=
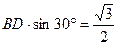 . ………………1分
. ………………1分②当△B D P2∽△BCO时,∠P2DB=∠OCB=90°.
在Rt△B P2D中,
DP2=
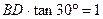 . ……………1分
. ……………1分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的扇形纸板,制作一个圆锥形的玩具帽,则帽子的底面半径
的扇形纸板,制作一个圆锥形的玩具帽,则帽子的底面半径 cm
cm
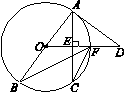
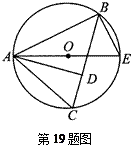
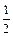 ,求AD的长.
,求AD的长.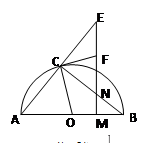
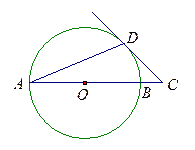
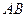 是⊙O的直径,
是⊙O的直径,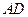 是弦,
是弦,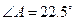 ,延长
,延长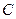 ,使得
,使得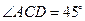 .
.
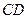 是⊙O的切线;
是⊙O的切线;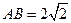 ,求
,求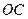 的长
的长
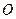 的直径,AD与⊙
的直径,AD与⊙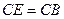

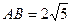 ,
,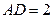 ,求线段BC的长
,求线段BC的长