题目内容
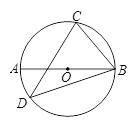
已知:如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF,CF,∠D=∠BFC.
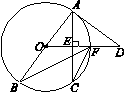
(1)求证:AD是⊙O的切线;
(2)若AC=8,tanB =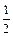 ,求AD的长.
,求AD的长.
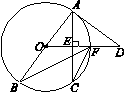
(1)求证:AD是⊙O的切线;
(2)若AC=8,tanB =
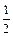 ,求AD的长.
,求AD的长.(1)证明略
(2)

(1)证明:∵ OD⊥AC于点E,
∴ ∠OEA=90°,∠1+∠2=90°.
∵ ∠D=∠BFC,∠BFC=∠1,
∴ ∠D +∠2=90°,∠OAD =90°.
∴ OA⊥AD于点A.………………………1分
∵OA是⊙O的半径,
∴AD是⊙O的切线. ……………………2分
(2)解:∵OD⊥AC于点E,AC是⊙O的弦,AC=8,
∴ .………………………………………………………3分
.………………………………………………………3分
∵∠B=∠C,tanB =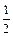 ,
,
∴ 在Rt△CEF中,∠CEF=90°,tanC =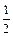 .
.
∴ .
.
设⊙O的半径为r,则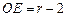 .
.
在Rt△OAE中,由勾股定理得 ,即
,即  .
.
解得 r =5.……………………………………………………………………4分
∴ 在Rt△OAE中, .
.
∴ 在Rt△OAD中, . ………………………5分
. ………………………5分
∴ ∠OEA=90°,∠1+∠2=90°.
∵ ∠D=∠BFC,∠BFC=∠1,
∴ ∠D +∠2=90°,∠OAD =90°.
∴ OA⊥AD于点A.………………………1分
∵OA是⊙O的半径,
∴AD是⊙O的切线. ……………………2分
(2)解:∵OD⊥AC于点E,AC是⊙O的弦,AC=8,
∴
 .………………………………………………………3分
.………………………………………………………3分∵∠B=∠C,tanB =
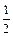 ,
,∴ 在Rt△CEF中,∠CEF=90°,tanC =
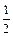 .
.∴
 .
.设⊙O的半径为r,则
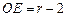 .
.在Rt△OAE中,由勾股定理得
 ,即
,即  .
.解得 r =5.……………………………………………………………………4分
∴ 在Rt△OAE中,
 .
.∴ 在Rt△OAD中,
 . ………………………5分
. ………………………5分
练习册系列答案
相关题目

 和半圆
和半圆 ,其中
,其中
 ,证明:
,证明: ;
;
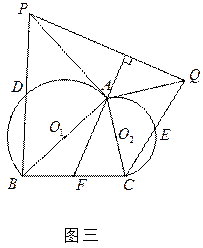
 内接于⊙O,
内接于⊙O, 是⊙O的切线,
是⊙O的切线, 的延长线交
的延长线交 .
.
 ,求⊙O的半径
,求⊙O的半径
 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由. 轴于D点,过点D作DF⊥AE于点F。
轴于D点,过点D作DF⊥AE于点F。
 、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 ▲ .
、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 ▲ .
 的代数式表示)
的代数式表示)