题目内容
如图,AB是半圆O的直径,C为半圆上一点,N是线段BC上一点(不与B﹑C重合),过N作AB的垂线交AB于M,交AC的延长线于E,过C点作半圆O的切线交EM于F,若NC∶CF=3∶2,则 sinB=______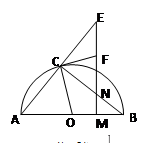


分析:由NC:CF=3:2,设NC=3x,则CF=2x,根据AB为直径可证BC⊥AE,因为CF为⊙O的切线,故OC⊥CF,利用互余关系可证∠OCB=∠ECF,∠B=∠E,而OB=OC,则∠OCB=∠B,故∠ECF=∠E,EF=CF=2x,同理可证∠FCN=∠FNC,FN=CF=2x,利用∠B=∠E,在Rt△CEN中,求sinE即可.
解:依题意,NC:CF=3:2,设NC=3x,则CF=2x,
∵AB为直径,∴BC⊥AE,
∵CF为⊙O的切线,∴OC⊥CF,
∵∠OCB+∠BCF=∠BCF+∠ECF=90°,
∴∠OCB=∠ECF,同理可证∠B=∠E,
∵OB=OC,∴∠OCB=∠B,
∴∠ECF=∠E,则EF=CF=2x,
同理可证∠FCN=∠FNC,则FN=CF=2x,
∴在Rt△CEN中,sinE=
 =
= =
= ,
,∴sinB=sinE=
 .
.故答案为
 .
.
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 的长为8,点
的长为8,点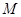 在线段
在线段 )上移动,则
)上移动,则 的取值范围是 .
的取值范围是 .

 ~
~ ;
; 的值;
的值;  的面积等于
的面积等于 ,求
,求 的度数.
的度数. 与坐标轴交于A(1,0)、B(5,0)两点,⊙
与坐标轴交于A(1,0)、B(5,0)两点,⊙

 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
 的值.
的值.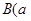 ,
,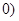 以
以 ,
, 的取值范围为
的取值范围为 
