题目内容
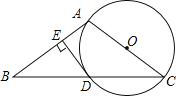
【题目】如图,AB是⊙O的直径,点C是⊙O外的一点,CB与⊙O相切于点B,AC交⊙O于点D,点E是![]() 上的一点(不与点A,B,D重合),若∠C=48°,则∠AED的度数为_____.
上的一点(不与点A,B,D重合),若∠C=48°,则∠AED的度数为_____.

【答案】48°或132°.
【解析】
先利用切线的性质及等边对等角求出∠CAB,∠ADO的度数,然后利用三角形内角和定理求出∠AOD的度数,然后分点E在![]() 上和点E在
上和点E在![]() 上两种情况,分别进行讨论即可.
上两种情况,分别进行讨论即可.
∵CB与⊙O相切于点B,
∴AB⊥BC,
∴∠ABC=90°,
∵∠C=48°,
∴∠CAB=90°﹣48°=42°,
连接OD,
∵OA=OD,
∴∠CAB=∠ADO=42°
∴![]()
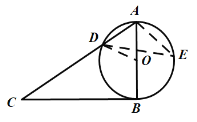
当点E在![]() 上时,
上时,
∠AED=![]() ,
,
当点E在![]() 上时,
上时,
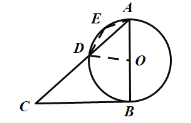
∠AED=180°﹣48°=132°,
故答案为:48°或132°.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某日王老师佩戴运动手环进行快走锻炼两次锻炼后数据如下表,与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的![]() 倍.设王老师第二次锻炼时平均步长减少的百分率为
倍.设王老师第二次锻炼时平均步长减少的百分率为![]() .注:步数
.注:步数![]() 平均步长
平均步长![]() 距离.
距离.
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) |
| ①_______ |
平均步长(米/步) |
| ②_______ |
距离(米) |
|
|
(1)根据题意完成表格;
(2)求![]() .
.