题目内容
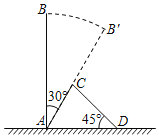
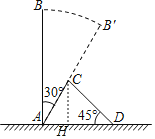
【题目】如图，某次台风来袭时，垂直于地面的大树AB被刮倾斜30°后，折断倒在地上，树的顶部恰好落在地面上点D处，大树被折断部分和地面所成的角∠ADC＝45°，AD＝4米，求这棵大树AB原来的高度是多少米？（结果精确到个位，参考数据：
，
，
）
【答案】这棵大树AB原来的高度是6.4米．
【解析】
过点C作CH⊥AD于点H，则∠ACH=30°，∠DCH=45°，解直角三角形即可得到结论．
过点C作CH⊥AD于点H，∠DCH=45°，
∵BA⊥AD，
∴BA∥CH，
∴∠ACH=∠BAC=30°，
设AH=x，则AC=2x，CH=HD=
x，
∴AD=AH+HD=x+x=4，
解得x=2﹣2，
∴AC=2x=4﹣4，HD=x=6-2，CD=
，
∴AB= A
=AC+C=AC+CD=4﹣4+
(米)，
答：这棵大树AB原来的高度是6.4米．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
