��Ŀ����
����Ŀ���ڡ�ABC�У���ACB��90�㣬BC��kAC����D��AC�ϣ�����BD��
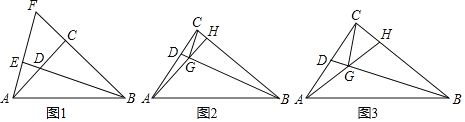
��1����ͼ1����k��1ʱ��BD���ӳ��ߴ�ֱ��AE������ΪE���ӳ�BC��AE���ڵ�F����֤��CD��CF��
��2������C��CG��BD������ΪG������AG���ӳ���BC�ڵ�H��
����ͼ2����CH��![]() CD��̽���߶�AG��GH��������ϵ���ú�k�Ĵ���ʽ��ʾ������֤����
CD��̽���߶�AG��GH��������ϵ���ú�k�Ĵ���ʽ��ʾ������֤����
����ͼ3������D��AC���е㣬ֱ��д��cos��CGH��ֵ���ú�k�Ĵ���ʽ��ʾ����
���𰸡���1��֤������������2����![]() ��֤������������cos��CGH=
��֤������������cos��CGH=![]() ��
��
��������
��1��ֻҪ֤����ACF�ա�BCD��ASA���������Ƴ�CF��CD��
��2�����ۣ�![]() ����CD��5a��CH��2a���������������ε��������AM��������ƽ���߷��߶γɱ����������ɽ�����⣮
����CD��5a��CH��2a���������������ε��������AM��������ƽ���߷��߶γɱ����������ɽ�����⣮
��3����ͼ3�У���AC��m����BC��km��![]() m����취֤����CGH����ABC���ɽ�����⣮
m����취֤����CGH����ABC���ɽ�����⣮
��1��֤������ͼ1�У�
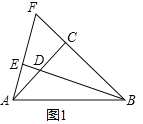
�ߡ�ACB��90�㣬BE��AF
���ACB����ACF����AEB��90��
�ߡ�ADE+��EAD����BDC+��DBC��90�㣬��ADE����BDC��
���CAF����DBC��
��BC��AC��
���ACF�ա�BCD��ASA����
��CF��CD��
��2���⣺���ۣ�![]() ��
��
���ɣ���ͼ2�У���AM��AC��CG���ӳ�����M��
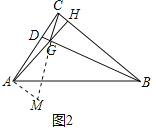
��CG��BD��MA��AC��
���CAM����CGD����BCD��90�㣬
���ACM+��CDG��90�㣬��ACM+��M��90�㣬
���CDB����M��
���BCD�ס�CAM��
��![]() ��k��
��k��
��CH��![]() CD����CD��5a��CH��2a��
CD����CD��5a��CH��2a��
��AM��![]() ��
��
��AM��CH��
��![]() ��
��
��![]() ��
��
��3���⣺��ͼ3�У���AC��m����BC��km��![]() m��
m��
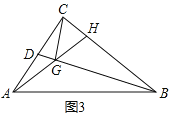
�ߡ�DCB��90�㣬CG��BD��
���DCG�ס�DBC��
��DC2��DGDB��
��AD��DC��
��AD2��DGDB��
��![]() ��
��
�ߡ�ADG����BDA��
���ADG�ס�BDA��
���DAG����DBA��
�ߡ�AGD����GAB+��DBA����GAB+��DAG����CAB��
�ߡ�AGD+��CGH��90�㣬��CAB+��ABC��90�㣬
���CGH����ABC��
��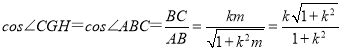 .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�