��Ŀ����
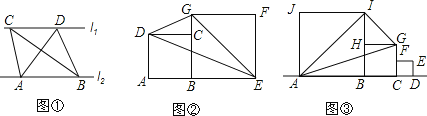
����Ŀ��̽������ͼ�٣�ֱ��l1��l2����A��B��ֱ��l1�ϣ���C��D��ֱ��l2�ϣ�����ABC�����ΪS1����ABD�����ΪS2����֤��S1��S2��
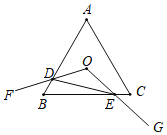
��չ����ͼ�ڣ�EΪ�߶�AB�ӳ�����һ�㣬BE��AB��������ABCD��������BEFG����ֱ��ABͬ�࣬��֤����DEG�������������BEFG�����һ�룮
Ӧ�ã���ͼ�ۣ���һ��ֱ���������е�A��B��C��D��������ABIJ��������BCGH��������CDEF����ֱ��ABͬ�࣬�ҵ�F��H�ֱ��DZ�CG��BI���е㣬��������CDEF�����Ϊl������AGI�����Ϊ�� ����
���𰸡�̽��������������չ����������Ӧ�ã�8![]()
��������
̽��������ƽ���ߵ����ʵõ���������������ͬ�ȸߵ����������Σ��������ǵ������ȣ�
��չ������BD�����������ε����ʿ�֪��GE��BD����DEG����BGEͬ�ȸߣ���S��DEG��S��BEG��������DEG�������������BEFG�����һ�룻
Ӧ�ã���������չ������˼·���н��
̽����֤������CM��l1�ڵ�M��DN��l1�ڵ�N����ͼ�٣�
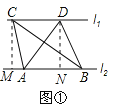
��l1��l2��
��CM��DN��
�֡ߡ�ABC����ABDͬ�ף�
��S1��S2��
��չ��֤��������BD����ͼ�ڣ�

���ı���ABCD���ı���BEFG��Ϊ�����Σ�
���ABD����BEG��45����
��BD��EG��
��̽���еĽ��ۿɵã�S��DEG��S��BEG��
��S��BEG��![]() S������BEFG��
S������BEFG��
��S��DEG��![]() S������BEFG��
S������BEFG��
Ӧ�ã��⣺������չ���ɵ�S��AGI��![]() S������ABIJ��
S������ABIJ��
��ͼ�ۣ�

��������CDEF�����Ϊl��
��CF��![]() ��
��
�ߵ�F��H�ֱ��DZ�CG��BI���е㣬
��BI��4![]() ����������ABIJ�ı߳�Ϊ4
����������ABIJ�ı߳�Ϊ4![]() ��
��
��S������ABIJ��16![]() ��
��
��S��AGI��8![]() ��
��
�ʴ��ǣ�8![]() ��
��

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�