题目内容
【题目】已知锐角△ABC中，边BC长为12，高AD长为8．
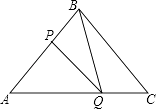
（1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K． 
①求 
的值；
②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值；
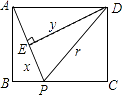
（2）若AB=AC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．
【答案】
（1）解：①∵EF∥BC，
∴ 
，
∴ 
= 
，
即 
的值是 
．
②∵EH=x，
∴KD=EH=x，AK=8﹣x，
∵ = ，
∴EF= 
，
∴S=EHEF= x（8﹣x）=﹣ 
+24，
∴当x=4时，S的最大值是24．
（2）解：设正方形的边长为a，
① 当正方形PQMN的两个顶点在BC边上时，
，
解得a= 
．
②当正方形PQMN的两个顶点在AB或AC边上时，
∵AB=AC，AD⊥BC，
∴BD=CD=12÷2=6，
∴AB=AC= 
，
∴AB或AC边上的高等于：
ADBC÷AB
=8×12÷10
= 
∴ 
，
解得a= 
．
综上，可得
正方形PQMN的边长是 或
【解析】（1）①根据EF∥BC，可得 ，所以 ，据此求出 的值是多少即可．②首先根据EH=x，求出AK=8﹣x，再根据 = ，求出EF的值；然后根据矩形的面积公式，求出S与x的函数关系式，利用配方法，求出S的最大值是多少即可．（2）根据题意，设正方形的边长为a，分两种情况：①当正方形PQMN的两个顶点在BC边上时；②当正方形PQMN的两个顶点在AB或AC边上时；分类讨论，求出正方形PQMN的边长各是多少即可．
【考点精析】通过灵活运用二次函数的最值和矩形的性质，掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；矩形的四个角都是直角，矩形的对角线相等即可以解答此题．
