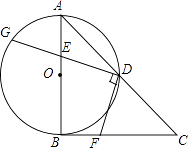Question

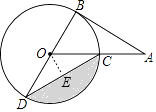
【题目】如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为（结果保留π）

Answer 1

【答案】 π﹣
【解析】解： 如图，过O作OE⊥CD于点E，
∵AB为⊙O的切线，
∴∠DBA=90°，
∵∠A=30°，
∴∠BOC=60°，
∴∠COD=120°，
∵OC=OD=2，
∴∠ODE=30°，
∴OE=1，CD=2DE=2
∴S阴影=S扇形COD﹣S△COD= ﹣ ×1×2 = π﹣ ，
所以答案是： π﹣ ．

【考点精析】解答此题的关键在于理解切线的性质定理的相关知识，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径，以及对扇形面积计算公式的理解，了解在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．