��Ŀ����
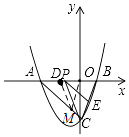
����Ŀ����ͼ��������y=ax2+bx��4��x�ύ��A����4��0����B��2��0�����㣬��y�ύ�ڵ�C������AC��BC��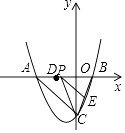
��1����������ߵĽ���ʽ��
��2������P��x���ϵ�һ���㣬��λ��AB֮�䣬����P��PE��AC����BC��E������CP����P�������Ϊx����PCE�����ΪS�������S����x�Ľ���ʽ�������PCE��������ֵ��
��3����ΪD����2��0��������M���߶�AC��һ���㣬�Ƿ����M�㣬��ʹ��OMD�ǵ��������Σ������ڣ���ֱ��д��M������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ѵ�A����4��0����B��2��0���ֱ�����У��ã� ![]() ��
��
��a= ![]() ��b=1��
��b=1��
��������κ�������ʽΪ ![]() ��C��0����4��
��C��0����4��
��2��
�⣺��P������Ϊ��x��0������BP=2��x��S��ABC= ![]()
��PE��AC��
���BPE=��BAC����BEP=��BCA��
���BPE�ס�BAC��
�� ![]() =��
=�� ![]() ��2������
��2������ ![]() =��
=�� ![]() ��2��
��2��
�� ![]() ��
��
�֡� ![]() ��
��
��S��PCE=S��BCP��S��BPE=2��2��x���� ![]() =
= ![]() ��
��
��x=��1ʱ����PCE��������ֵΪ3
��3��
�⣺����M�㣮����ͼ������D��DM��ֱx�ύAC��M��
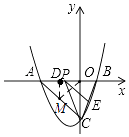
��A����4��0����C����4��0����
��DM=AD=2=DO��
��M����2����2����
����ͼ����DO���д��߽�AC�ڵ�M����MD=MO��
��A��C���������֪AC�Ľ���ʽΪy=��x��4��
��x=��1����ɵ�y=��3��
��M����1����3����
������������M����������1����3����2����2��
����������1����A��B��������������ʽֱ�����a��b���ɣ���2�����P������꣬����PE��AC�����BPE�͡�BAC���ƣ���������������Ʊȵ�ƽ���ó���BPE���������ʽ���á�PCB�������ȥ��BPE���������S���������䷽������ֵ���ɣ���3��������������ۣ���DO=DM����MD=MO��
�����㾫����������Ĺؼ�����������κ����ĸ�������֪ʶ������һ��أ��Ա���x�������y֮��������¹�ϵ��һ��ʽ��y=ax2+bx+c(a��0��a��b��cΪ����)�����yΪx�Ķ��κ������Լ��Զ��κ�����ͼ������⣬�˽���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ����ѧ������ѧϰϰ�ߣ�ijѧУ�ƻ�����һ�Ρ��������⼯����չʾ����Ը�У����ѧ�����������⼯�������������һ�γ������飬�����ռ������ݻ��������治������ͳ��ͼ���������ͼ�����ṩ����Ϣ������������⣺
������� | Ƶ�� | Ƶ�� |
�dz��� | 0.21 | |
�Ϻ� | 70 | |
һ�� | ||
���� | 36 |
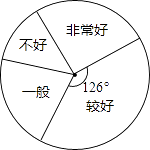
��1�����γ����������˶���ѧ����
��2����ȫͳ�Ʊ�����ȱ�����ݣ�
��3����У��1500��ѧ�������Ƹ�Уѧ���������⼯������dz��á��͡��Ϻá���ѧ��һ��Լ��������
��4��ijѧϰС��4��ѧ���Ĵ��⼯�У���2�����dz��á�����ΪA1��A2����1�����Ϻá�����ΪB����1����һ�㡱����ΪC������Щ���⼯������������������״����С����ɫ�����������ȫ��ͬ�����г�ȡһ�������Żأ������µ�3�����⼯���ٳ�ȡһ�������á��б�����������ͼ���ķ���������γ鵽�Ĵ��⼯���ǡ��dz��á��ĸ��ʣ�