题目内容
边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在抛物线y=ax2(a<0)的图象上.则抛物线y=ax2的函数解析式为( )

A.y=--
| B.y=-
| C.y=-2x2 | D.y=-
|

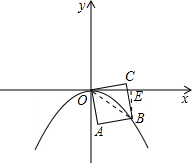
如图,作BE⊥x轴于点E,连接OB,
∵正方形OABC绕顶点O顺时针旋转75°,
∴∠AOE=75°,
∵∠AOB=45°,
∴∠BOE=30°,
∵OA=1,
∴OB=
,
∵∠OEB=90°,
∴BE=
OB=
,
∴OE=
,
∴点B坐标为(
,-
),
代入y=ax2(a<0)得a=-
,
∴y=-
x2.
故选B.
∵正方形OABC绕顶点O顺时针旋转75°,
∴∠AOE=75°,
∵∠AOB=45°,
∴∠BOE=30°,
∵OA=1,
∴OB=
| 2 |
∵∠OEB=90°,
∴BE=
| 1 |
| 2 |
| ||
| 2 |
∴OE=
| ||
| 2 |
∴点B坐标为(
| ||
| 2 |
| ||
| 2 |
代入y=ax2(a<0)得a=-
| ||
| 3 |
∴y=-
| ||
| 3 |
故选B.


练习册系列答案
相关题目
 的图像与
的图像与 轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。
轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。