题目内容
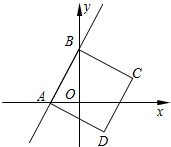
如图,一次函数y=2x+4的图象与x、y轴分别相交于点A、B,四边形ABCD是正方形.
(1)求点A、B、D的坐标;
(2)求直线BD的表达式.
(1)求点A、B、D的坐标;
(2)求直线BD的表达式.

(1)∵当y=0时,2x+4=0,x=-2.
∴点A(-2,0).(1分)
∵当x=0时,y=4.
∴点B(0,4).(1分)
过D作DH⊥x轴于H点,(1分)
∵四边形ABCD是正方形,
∴∠BAD=∠AOB=∠AHD=90°,AB=AD.(1分)
∴∠BAO+∠ABO=∠BAO+∠DAH,
∴∠ABO=∠DAH.(1分)
∴△ABO≌△DAH.(1分)
∴DH=AO=2,AH=BO=4,
∴OH=AH-AO=2.
∴点D(2,-2).(1分)
(2)设直线BD的表达式为y=kx+b.(1分)
∴
(1分)
解得
,
∴直线BD的表达式为y=-3x+4.(1分)

∴点A(-2,0).(1分)
∵当x=0时,y=4.
∴点B(0,4).(1分)
过D作DH⊥x轴于H点,(1分)
∵四边形ABCD是正方形,
∴∠BAD=∠AOB=∠AHD=90°,AB=AD.(1分)
∴∠BAO+∠ABO=∠BAO+∠DAH,
∴∠ABO=∠DAH.(1分)
∴△ABO≌△DAH.(1分)
∴DH=AO=2,AH=BO=4,
∴OH=AH-AO=2.
∴点D(2,-2).(1分)
(2)设直线BD的表达式为y=kx+b.(1分)
∴
|
解得
|
∴直线BD的表达式为y=-3x+4.(1分)


练习册系列答案
相关题目




 路程随时间变化关系如图所示:
路程随时间变化关系如图所示: