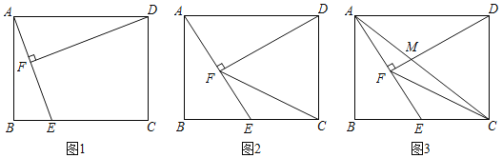
题目内容
【题目】图![]() 、图
、图![]() 均是
均是![]() 的正方形网格,每个小正方形的顶点称为格点,
的正方形网格,每个小正方形的顶点称为格点,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 为边
为边![]() 的中点.分别在图
的中点.分别在图![]() 、图
、图![]() 中
中![]() 的边
的边![]() 上确定点
上确定点![]() 并作出直线
并作出直线![]() ,使
,使![]() 与
与![]() 相似.
相似.
要求:(1)图![]() 、图
、图![]() 中的点
中的点![]() 位置不同.
位置不同.
(2)只用无刻度的直尺,保留适当的作图痕迹.
【答案】答案见解析
【解析】
(1)找到格点N、M,连接NM交AB于点P,过P点和D点作直线PD,P点即为所求,理由是:找到格点Q,连接NQ交AB于点T,连接TP,根据三角形相似的判定和性质,得到PT和AP的长,根据勾股定理和中点的性质,计算AD的长,再根据相似三角形的判定方法即可解决.
(2)找到格点K、L,连接KL与AB变动边的交点即为所求P点,理由为:根据三角形全等的判定和性质,证明P点为AB边的中点,然后根据中位线的意义和性质,结合三角形相似的判定方法,即可得出△APD∽△ABC;
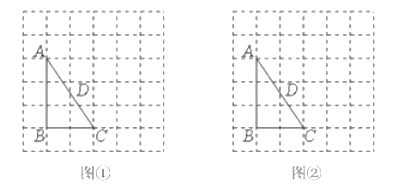
解:(1)如图:找到格点N、M,连接NM交AB于点P,过P点和D点作直线PD,此时△APD∽△ACB.理由如下:
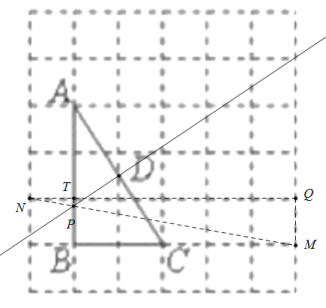
找到格点N、M、Q,连接NM交AB于点P,连接NQ交AB于点T,连接TP,由图可知,∠NTP=∠NQM,∠QNM=∠TNP,
∴△TNP∽△QNM,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
D为AC的中点,
∴![]() ,
,
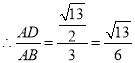 ,
,
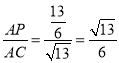 ,
,
在△APD和△ACB中,
∠DAP=∠BAC,
![]() ,
,
∴△APD∽△ACB.
(2)如图:找到格点K,L,连接KL,交AB于点P,过P点和D点作直线PD,此时△ABC∽△APD.理由如下:
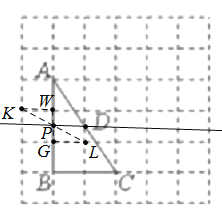
找到格点W、G,连接WG,KW,GL,由图可知,KW∥GL,
∴∠KPW=∠LPG,∠KWP=∠LGP,
又∵KW=LG,
∴△KWG≌LGP,
∴WP=GP,
∴P为WG的中点,
∵AW+WP=BG+GP,
∴AP=BP,
∴P为AB的中点,
∵D点为AC的中点,
∴PD为△ABC的中位线,
∴PD∥BC,
∴△APD∽△ABC.

【题目】某校鼓励师生利用课余时间广泛阅读,为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下单位:min)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
分段整理样本数据:
课外阅读时间 |
|
|
|
|
等级 | D | C | B | A |
人数 | 3 | ① | 8 | ② |
统计量:
平均数 | 中位数 | 众数 |
80 | ③ | ④ |
得出结论:
(1)填写表格中的数据:
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?