题目内容
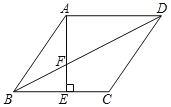
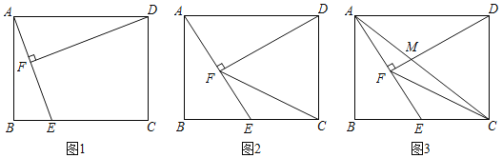
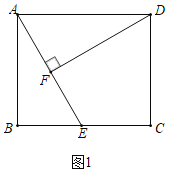
【题目】如图1,在矩形ABCD中,E是边BC上一点,连接AE,过点D作DF⊥AE于点F.
(1)若AE=DA,求证:△ABE≌△DFA.
(2)若AB=6,AD=8,且E为BC中点.
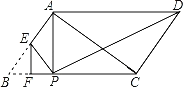
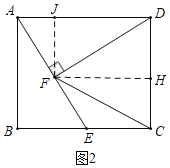
①如图2,连接CF,求sin∠DCF的值.
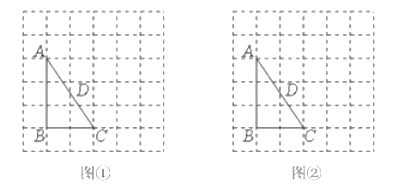
②如图3,连接AC交DF于点M,求CM:AM的值.
【答案】(1)见解析;(2)①![]() ,②
,②![]()
【解析】
(1)根据AAS证明三角形全等即可;
(2)①如图2中,过点F作FH⊥CD于H,FJ⊥AD于J.利用相似三角形的性质求出AF,DF,解直角三角形求出FJ,DJ,CH,FH即可解决问题;
②如图3中,延长DF交CB的延长线于K.利用相似三角形的性质求出KE,再利用平行线分线段成比例定理求解即可.
(1)证明:如图1中,
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠B=∠AFD=90°,
在△ABE和△DFA中
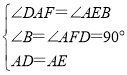 ,
,
∴△ABE≌△DFA(AAS).
(2)①解:如图2中,过点F作FH⊥CD于H,FJ⊥AD于J.
∵四边形ABCD是矩形,AB=CD=6,BC=AD=8,
∴∠B=90°,
∵BE=EC=4,
∴AE=![]() =
=![]() =2
=2![]() ,
,
∵∠DAF=∠AEB,∠B=∠AFD=90°,
∴△ABE∽△DFA,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴DF=![]() ,AF=
,AF=![]() ,
,
∵FJ⊥AD,
∴FJ=DH=![]() =
=![]() ,DJ=FH=
,DJ=FH=![]() =
=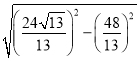 =
=![]() ,
,
∴CH=CD﹣DH=6﹣![]() =
=![]() ,
,
∴CF=![]() =
=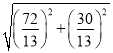 =6,
=6,
∴sin∠DCF=![]() =
=![]() =
=![]() .
.
②解:如图3中,延长DF交CB的延长线于K.
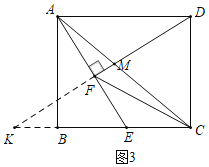
∵∠KEF=∠AEB,∠EFK=∠ABE=90°,
∴△KEF∽△AEB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴KE=5,
∴CK=KE+EC=9,
∵AD∥CK,
∴![]() =
=![]() =
=![]() .
.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目