题目内容
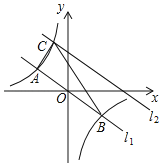
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是-4;
的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是-4;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x﹤
x﹤![]() 的解集;
的解集;
(3)将直线l1:y=![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为20,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为20,求平移后的直线l2的函数表达式.
【答案】(1)![]() (2)x>4或-4<x<0 (3)y=﹣
(2)x>4或-4<x<0 (3)y=﹣![]() x+5
x+5
【解析】
(1)由正比例函数解析式确定A(-4,2),然后把A点坐标代入y=![]() 中求出k得到反比例函数解析式;
中求出k得到反比例函数解析式;
(2)通过解方程组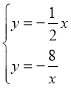 得B(4,-2),然后利用函数图象写出反比例函数图象在一次函数y=-
得B(4,-2),然后利用函数图象写出反比例函数图象在一次函数y=-![]() x上方所对应的自变量的范围,从而得到-
x上方所对应的自变量的范围,从而得到-![]() x<
x<![]() 的解集;
的解集;
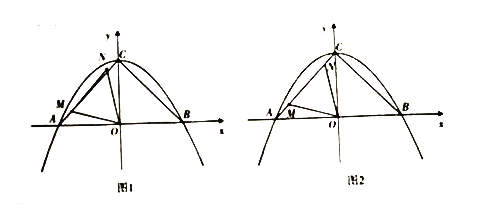
(3)设直线l2交x轴于D,连接AD、BD,如图,利用三角形面积公式得S△ADB=S△ACB=20,则![]() ×OD×2+
×OD×2+![]() ×OD×2=30,求出OD得到D(10,0),利用两直线平行可设直线l2的解析式为y=-
×OD×2=30,求出OD得到D(10,0),利用两直线平行可设直线l2的解析式为y=-![]() x+b,然后把D点坐标代入求出b得到直线l2的解析式为y=-
x+b,然后把D点坐标代入求出b得到直线l2的解析式为y=-![]() x+5.
x+5.
解:(1)∵直线l1:y=﹣![]() x经过点A,A点的横坐标是-4
x经过点A,A点的横坐标是-4
∴当x=﹣4时,y=2,
∴A(﹣4,2),
∵反比例函数y=![]() 的图象经过点A,
的图象经过点A,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为y=﹣![]() ;
;
(2)解方程组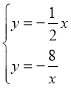 得
得![]() 或
或![]() ,
,
∴B(4,﹣2),
∴不等式﹣![]() x﹤
x﹤![]() 的解集为xspan>>4或-4<x<0;
的解集为xspan>>4或-4<x<0;
(3)如图,设平移后的直线l2与x轴交于点D,连接AD,BD,
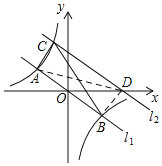
∵CD∥AB,
∴△ABC的面积与△ABD的面积相等,
∵△ABC的面积为20,
∴S△AOD+S△BOD=20,即![]() OD(|yA|+|yB|)=20,
OD(|yA|+|yB|)=20,
∴![]() ×OD×4=20,
×OD×4=20,
∴OD=10,
∴D(10,0),
设平移后的直线l2的函数表达式为y=﹣![]() x+b,
x+b,
把D(10,0)代入,可得0=﹣![]() ×10+b,
×10+b,
解得b=5,
∴平移后的直线l2的函数表达式为y=﹣![]() x+5.
x+5.