题目内容
【题目】如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于 E,过 E 做 EF⊥AD 于 F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF 是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠FAB=∠ABE=90°,AF∥BE,
∵EF⊥AD,
∴∠FAB=∠ABE=∠AFE=90°,
∴四边形ABEF是矩形,
∵AE平分∠BAD,AF∥BE,
∴∠FAE=∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是正方形.
(2)
解:过点P作PH⊥AD于H,如图所示:
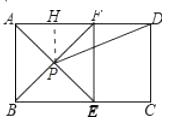
∵四边形ABEF是正方形,
∴BP=PF,BA⊥AD,∠PAF=45°,∴AB∥PH,
∵AB=6,∴AH=PH=3,
∵AD=8,∴DH=AD﹣AH=8﹣3=5,
在Rt△PHD中,∠PHD=90°.
∴tan∠ADP=![]() =
=![]()
【解析】(1)根据正方形的判定定理,先证明四边形ABEF是矩形,再证明邻相等可得其为正方形;
(2)求tan∠ADP需要构造直角三角形,所以过点P作PH⊥AD于H,从而可找到突破口.

练习册系列答案
相关题目