题目内容
【题目】如图,抛物线 ![]() 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).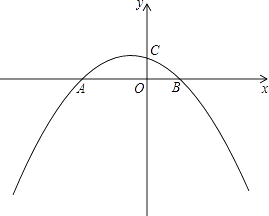
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN﹣CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.
【答案】
(1)
解:∵抛物线y=ax2﹣ ![]() x+2经过点B(3,0),
x+2经过点B(3,0),
∴9a﹣ ![]() ×3+2=0,
×3+2=0,
解得a=﹣ ![]() ,
,
∴y=﹣ ![]() x2﹣
x2﹣ ![]() x+2,
x+2,
∵y=﹣ ![]() x2﹣
x2﹣ ![]() x+2=﹣
x+2=﹣ ![]() (x2+3x)+2=﹣
(x2+3x)+2=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() ,
,
∴顶点坐标为(﹣ ![]() ,
, ![]() )
)
(2)
解:∵抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2的对称轴为直线x=﹣
x+2的对称轴为直线x=﹣ ![]() ,
,
与x轴交于点A和点B,点B的坐标为(3,0),
∴点A的坐标为(﹣6,0).
又∵当x=0时,y=2,
∴C点坐标为(0,2).
设直线AC的解析式为y=kx+b,
则 ![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y= ![]() x+2.
x+2.
∵S△AMC=S△ABC,
∴点B与点M到AC的距离相等,
又∵点B与点M都在AC的下方,
∴BM∥AC,
设直线BM的解析式为y= ![]() x+n,
x+n,
将点B(3,0)代入,得 ![]() ×3+n=0,
×3+n=0,
解得n=﹣1,
∴直线BM的解析式为y= ![]() x﹣1.
x﹣1.
由 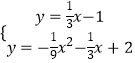 ,解得
,解得 ![]() ,
, ![]() ,
,
∴M点的坐标是(﹣9,﹣4)

(3)
解:在抛物线对称轴上存在一点N,能够使d=|AN﹣CN|的值最大.理由如下:
∵抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于点A和点B,
x+2与x轴交于点A和点B,
∴点A和点B关于抛物线的对称轴对称.
连接BC并延长,交直线x=﹣ ![]() 于点N,连接AN,则AN=BN,此时d=|AN﹣CN|=|BN﹣CN|=BC最大.
于点N,连接AN,则AN=BN,此时d=|AN﹣CN|=|BN﹣CN|=BC最大.
设直线BC的解析式为y=mx+t,将B(3,0),C(0,2)两点的坐标代入,
得 ![]() ,
,  ,
,
∴直线BC的解析式为y=﹣ ![]() x+2,
x+2,
当x=﹣ ![]() 时,y=﹣
时,y=﹣ ![]() ×(﹣
×(﹣ ![]() )+2=3,
)+2=3,
∴点N的坐标为(﹣ ![]() ,3),d的最大值为BC=
,3),d的最大值为BC= ![]() =
= ![]() .
.
【解析】(1)先把点B的坐标代入y=ax2﹣ ![]() x+2,可求得a的值,再利用配方法将一般式化为顶点式,即可求得抛物线的顶点坐标;(2)先由抛物线的解析式y=﹣
x+2,可求得a的值,再利用配方法将一般式化为顶点式,即可求得抛物线的顶点坐标;(2)先由抛物线的解析式y=﹣ ![]() x2﹣
x2﹣ ![]() x+2,求出与x轴的交点A的坐标,与y轴的交点C的坐标,再由△AMC与△ABC的面积相等,得出这两个三角形AC边上的高相等,又由点B与点M都在AC的下方,得出BM∥AC,则点M既在过B点与AC平行的直线上,又在抛物线y=﹣
x+2,求出与x轴的交点A的坐标,与y轴的交点C的坐标,再由△AMC与△ABC的面积相等,得出这两个三角形AC边上的高相等,又由点B与点M都在AC的下方,得出BM∥AC,则点M既在过B点与AC平行的直线上,又在抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2上,所以先运用待定系数法求出直线AC的解析式为y=
x+2上,所以先运用待定系数法求出直线AC的解析式为y= ![]() x+2,再设直线BM的解析式为y=
x+2,再设直线BM的解析式为y= ![]() x+n,将点B(3,0)代入,求出n的值,得到直线BM的解析式为y=
x+n,将点B(3,0)代入,求出n的值,得到直线BM的解析式为y= ![]() x﹣1,然后解方程组
x﹣1,然后解方程组 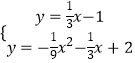 ,即可求出点M的坐标;(3)连接BC并延长,交抛物线的对称轴x=﹣
,即可求出点M的坐标;(3)连接BC并延长,交抛物线的对称轴x=﹣ ![]() 于点N,连接AN,根据轴对称的性质得出AN=BN,并且根据三角形三边关系定理得出此时d=|AN﹣CN|=|BN﹣CN|=BC最大.运用待定系数法求出直线BC的解析式,再将x=﹣
于点N,连接AN,根据轴对称的性质得出AN=BN,并且根据三角形三边关系定理得出此时d=|AN﹣CN|=|BN﹣CN|=BC最大.运用待定系数法求出直线BC的解析式,再将x=﹣ ![]() 代入,求出y的值,得到点N的坐标,然后利用勾股定理求出d的最大值BC即可.
代入,求出y的值,得到点N的坐标,然后利用勾股定理求出d的最大值BC即可.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案【题目】当前,“校园手机”现象已经受到社会广泛关注,某数学兴趣小组对“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理: 频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |

(1)请求出共调查了多少人;并把小文整理的图表补充完整;
(2)小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?
【题目】当前,“校园手机”现象已经受到社会广泛关注,某数学兴趣小组对“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理: 频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |

(1)请求出共调查了多少人;并把小文整理的图表补充完整;
(2)小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?