题目内容
【题目】如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈ ![]() ,cos53°≈
,cos53°≈ ![]() ,tan53°≈
,tan53°≈ ![]() ,
, ![]() ≈1.41)
≈1.41)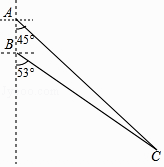
【答案】解:如图作CE⊥AB于E.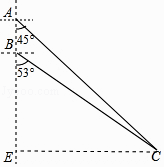
在Rt△ACE中,∵∠A=45°,
∴AE=EC,设AE=EC=x,则BE=x﹣5,
在Rt△BCE中,
∵tan53°= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x=20,
∴AE=EC=20,
∴AC=20 ![]() =28.2,
=28.2,
BC= ![]() =25,
=25,
∴A船到C的时间≈ ![]() =0.94小时,B船到C的时间=
=0.94小时,B船到C的时间= ![]() =1小时,
=1小时,
∴C船至少要等待0.94小时才能得到救援
【解析】如图作CE⊥AB于E.设AE=EC=x,则BE=x﹣5,在Rt△BCE中,根据tan53°= ![]() ,可得
,可得 ![]() =
= ![]() ,求出x,再求出BC、AC,分别求出A、B两船到C的时间,即可解决问题.
,求出x,再求出BC、AC,分别求出A、B两船到C的时间,即可解决问题.
【考点精析】通过灵活运用关于方向角问题,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角即可以解答此题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】当前,“校园手机”现象已经受到社会广泛关注,某数学兴趣小组对“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理: 频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |
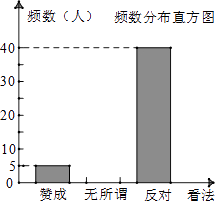
(1)请求出共调查了多少人;并把小文整理的图表补充完整;
(2)小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?