题目内容
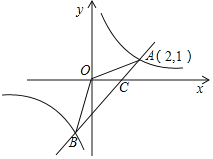
【题目】
图象与
轴交于
，与
轴交于
，所有符合条件的函数解析式共有___个.
【答案】
【解析】
利用已知条件可得到A（-2，0），B（1，0），C（0，1）或A（-2，0），B（1，0），C（0，-1）或A（2，0），B（-1，0），C（0，1）或A（2，0），B（-1，0），C（0，-1）或A（2，0），B（1，0），C（0，-1）或A（2，0），B（1，0），C（0，1）或A（-2，0），B（-1，0），C（0，-1）或A（-2，0），B（-1，0），C（0，1）然后利用交点式分别求四种情况下的抛物线解析式．
解：∵OA=2，OB=1，OC=1，
∴A（-2，0），B（1，0），C（0，1）或A（-2，0），B（1，0），C（0，-1）或A（2，0），B（-1，0），C（0，1）或A（2，0），B（-1，0），C（0，-1），
当A（-2，0），B（1，0），C（0，1），设抛物线解析式为y=a（x+2）（x-1），把C（0，1）代入得a2（-1）=1，解得a=-
，所以抛物线解析式为y=-（x+2）（x-1）=-x2-x+1；
当A（-2，0），B（1，0），C（0，-1），设抛物线解析式为y=a（x+2）（x-1），把C（0，-1）代入得a2（-1）=-1，解得a=，所以抛物线解析式为y=（x+2）（x-1）=x2+x-1；
当A（2，0），B（-1，0），C（0，1），设抛物线解析式为y=a（x-2）（x+1），把C（0，1）代入得a（-2）1=1，解得a=-，所以抛物线解析式为y=-（x-2）（x+1）=-x2+x+1；
当A（2，0），B（-1，0），C（0，-1），设抛物线解析式为y=a（x-2）（x+1），把C（0，-1）代入得a（-2）1=-1，解得a=，所以抛物线解析式为y=（x-2）（x+1）=x2-x-1；
当A（2，0），B（1，0），C（0，-1）时，设抛物线解析式为y=a（x-2）（x-1），把C（0，-1）代入得，
a（-2）（-1）=-1，解得a=-，所以抛物线解析式为y=-（x-2）（x-1）=-x2-
x-1；
同理可得，当A（2，0），B（1，0），C（0，1）时，抛物线解析式为y=x2+x+1；
当A（-2，0），B（-1，0），C（0，-1）时，抛物线解析式为y=-x2-x-1；
当A（-2，0），B（-1，0），C（0，1）时，抛物线解析式为y=x2+x+1；
∴函数解析式为y=-xspan>2-x+1或y=x2+x-1或y=-x2+x+1或y=x2-x-1或y=-x2-x-1或y=x2+x+1或y=-x2-x-1或y=x2+x+1．
故答案为：8.
