题目内容
【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其顶点
,其顶点![]() 的坐标为
的坐标为![]() 为抛物线上
为抛物线上![]() 轴下方一点.
轴下方一点.
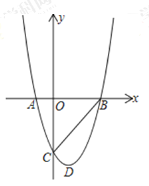
(1)求抛物线的解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若直线![]() 与抛物线交于
与抛物线交于![]() 两点,问:是否存在
两点,问:是否存在![]() 的值,使得
的值,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)由于已知抛物线顶点坐标,故可设顶点式,再把点B坐标代入求得a,即求得抛物线解析式;
(2)先根据抛物线解析式求出A、C坐标.由∠PCB=∠ACB和∠ABC=45°联想到构造△ABC的全等三角形,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,构造角边角得到的△ABC≌△MBC,进而求得点M坐标.求直线CM解析式,把直线CM与抛物线解析式联立方程组,求得的其中一解即为点P坐标;
,构造角边角得到的△ABC≌△MBC,进而求得点M坐标.求直线CM解析式,把直线CM与抛物线解析式联立方程组,求得的其中一解即为点P坐标;
(3)假设存在![]() 的值,使直线
的值,使直线![]() 与(1)中所求的抛物线
与(1)中所求的抛物线![]() 交于
交于![]() 、
、![]() ,联立两函数解析式求出
,联立两函数解析式求出![]() ,根据OM2+ON2=MN2,整理后把x1+x2和x1·x2的值代入即可求出a的值.
,根据OM2+ON2=MN2,整理后把x1+x2和x1·x2的值代入即可求出a的值.
(1)设抛物线解析式为y=a(x-1)2-4,把B(3,0)代入得,
![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,
,
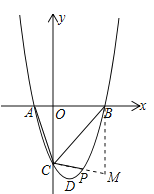
∵y=0时,x2-2x-3=0,
解得:x1=-1,x2=3,
∴A(-1,0),AB=3-(-1)=4,
∵x=0时,y=x2-2x-3=-3,
∴C(0,-3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°.
∵OC∥BM,
∴∠MBC=∠OCB=∠OBC=45°,
在△ABC与△MBC中,
 ,
,
∴△ABC≌△MBC(ASA)
![]() ,
,
![]() ,
,
设CM解析式为y=kx+b,
把C(0,-3),![]() 代入,得
代入,得
![]() ,
,
∴ ,
,
![]() ,
,
由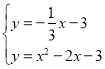 ,得
,得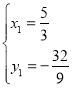 或
或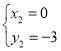 (舍),
(舍),
![]() ;
;
(3)假设存在![]() 的值,使直线
的值,使直线![]() 与(1)中所求的抛物线
与(1)中所求的抛物线![]() 交于
交于![]() 、
、![]() ,
,
两点(![]() 在
在![]() 的左侧),使得
的左侧),使得![]() ,
,
由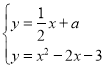 得
得![]() ,
,
![]() ,
,
又![]() ,
,
![]()
![]() ,
,
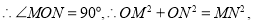
![]() ,
,
![]() ,
,
![]() 即
即![]() ,
,
![]() ,
,
![]() 存在
存在![]() 使得
使得![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目