题目内容
【题目】已知正六边形ABCDEF,如图所示,其外接圆的半径是a,求正六边形的周长和面积.
【答案】6a ; ![]()
【解析】试题分析:
如图,
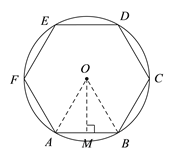
连接OA、OB,过点O作OM⊥AB于点M,由题意易证△OAB是等边三角形,从而得到AB=a,可得正六边形周长为6a;再由“等腰三角形的三线合一或垂径定理”可得AM= ![]() ,结合勾股定理可求得OM,即可求△OAB的面积,再求正六边形的面积.
,结合勾股定理可求得OM,即可求△OAB的面积,再求正六边形的面积.
试题解析:
如图,连接OA、OB,过点O作OM⊥AB于点M,
∵六边形ABCDEF是正六边形,
∴∠AOB=![]() ,
,
∵OA=OB,
∴△OAB是等边三角形,
∴AB=a=BC=CD=DE=EF=FA,
∴C正六边形ABCDEF=6a;
∵OM⊥AB于点M,△OAB是等边三角形,
∴AM= ![]() ,
,
∴OM= ![]() ,
,
∴S△OAB=![]() ,
,
∴S正六边形ABCDEF=6 S△OAB=![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目