题目内容
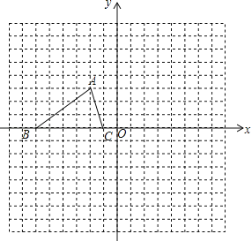
【题目】如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为_______.

【答案】![]()
【解析】由已知条件,易证四边形CDME是矩形,则DE=CM,由于无法直接求出DE的最小值,故可通过求CM的最小值进行解答;
由垂线段最短可知,当CM⊥AB时,CM取得最小值,在Rt△ABC中,由等面积法计算出CM的长度,问题即可解答.
如下图所示,连接CM.

∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°.
∵∠ACB=90°,
∴四边形CDME是矩形,
∴DE=CM.
∵∠ACB=90°,BC=5,AC=12,
∴AB=![]() .
.
当CM⊥AB时,CM最短,此时△ABC的面积=![]() AB·CM=
AB·CM=![]() BC·AC=30,
BC·AC=30,
∴CM的最小值=![]() .
.
∴线段DE的最小值为![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目