题目内容
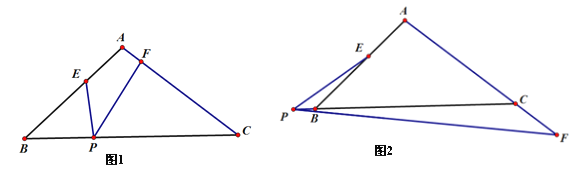
【题目】如图，在三角形ABC中，已知AC⊥BC，CD⊥AB，∠1=∠2．对于下列五个结论：
①DE∥AC；
②∠1=∠B；
③∠3=∠A；
④∠3=∠EDB；
⑤∠2与∠3互补．
其中正确的有（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】C
【解析】
由同角的余角相等得到∠1=∠B，由已知内错角相等得到AC与DE平行，由同角的余角相等可得③④正确，∠2与∠3互余，由此即可判断．
解：∵∠1=∠2，
∴AC∥DE，故①正确；
∵AC⊥BC，CD⊥AB，
∴△ACD与△ACB都为直角三角形，
∴∠A+∠1=90°，∠A+∠B=90°，
∴∠1=∠B，故②正确，
∵∠A+∠1=90°，∠1+∠3=90°
∴∠A=∠3，故③正确；
∵∠1+∠3=90°，∠1=∠2
∴∠2+∠3=90°，
∵∠2+∠EDB=90°，
∴∠3=∠EDB，故④正确，
∵∠2+∠3=90°，
∴∠2与∠3互余，故⑤错误；
故选：C．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
【题目】（1）先完成下列表格：
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | ______ | 1 | ______ | ______ | …… |
（2）由上表你发现什么规律？
（3）根据你发现的规律填空：
①已知
=1.732则
=______
=______
②已知
=0.056，则
=______
