题目内容
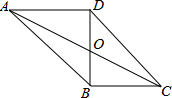如图，已知四边形ABCD为平行四边形，AD⊥BD，AC交BD于0，AD=8，AB=1O，求BC，CD，OC的长．考点：平行四边形的性质
专题：
分析：根据平行四边形对边相等的性质即可求出BC和CD的长度，然后运用勾股定理求出BD的长度，根据平行四边形对角线互相平分的性质求出BO的长度，最后运用勾股定理求出OC的长度．
解答：解：∵四边形ABCD是平行四边形，
∴AD=BC，AB=CD，
∵AD=8，AB=1O，
∴BC=8，CD=10，
∵AD⊥BD，
∴BD=
=6，
∴OB=
BD=3，
则OC=
=
．
∴AD=BC，AB=CD，
∵AD=8，AB=1O，
∴BC=8，CD=10，
∵AD⊥BD，
∴BD=
| AB2-AD2 |
∴OB=
| 1 |
| 2 |
则OC=
| OB2+BC2 |
| 73 |
点评：本题考查了平行四边形的性质以及勾股定理的应用，注意掌握：平行四边形的对边相等；平行四边形的对角线互相平分．
练习册系列答案
相关题目
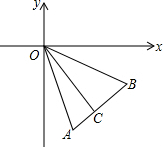如图，在平面直角坐标系中，A、B两点分别位于第四象限，且∠AOB=45°，OC⊥AB于C，把△AOC沿直线OA翻折后，OC边恰好落在y轴上，若AC=1，OC=3，求经过点A的双曲线和B点坐标．
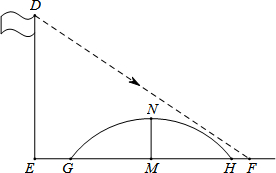相山区实验中学数学兴趣小组在周末开展研究性学习，测算小桥所在圆的半径．他们发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上（如图），此时此刻，身高1.6米的海涛，测得自己的影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径．
如图，直线y=x+1与y轴交于A点，与反比例函数
如图，在平面直角坐标系xOy中，直线y=mx+1与双曲线
如图，在△ABC中，AE平分∠BAC（∠C＞∠B），F为AE上的一点，且FD⊥BC于D，则∠EFD与∠B，∠C的关系是