题目内容
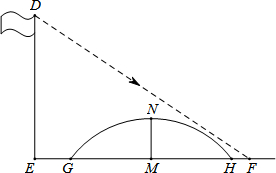 相山区实验中学数学兴趣小组在周末开展研究性学习,测算小桥所在圆的半径.他们发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上(如图),此时此刻,身高1.6米的海涛,测得自己的影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
相山区实验中学数学兴趣小组在周末开展研究性学习,测算小桥所在圆的半径.他们发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上(如图),此时此刻,身高1.6米的海涛,测得自己的影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.考点:相似三角形的应用,勾股定理,垂径定理的应用
专题:
分析:根据已知得出旗杆高度,进而得出GM=MH,再利用勾股定理求出半径即可.
解答: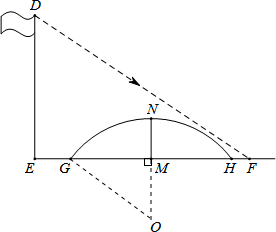 解:∵海涛身高1.6米,测得其影长为2.4米,
解:∵海涛身高1.6米,测得其影长为2.4米,
∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12-3-1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r-2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r-2)2+16,
解得:r=5.
答:小桥所在圆的半径为5m.
 解:∵海涛身高1.6米,测得其影长为2.4米,
解:∵海涛身高1.6米,测得其影长为2.4米,∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12-3-1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r-2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r-2)2+16,
解得:r=5.
答:小桥所在圆的半径为5m.
点评:此题主要考查了垂径定理以及勾股定理的应用,根据已知得出关于r的等式是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
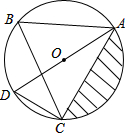 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°.请解答下列问题:
如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°.请解答下列问题: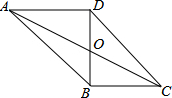 如图,已知四边形ABCD为平行四边形,AD⊥BD,AC交BD于0,AD=8,AB=1O,求BC,CD,OC的长.
如图,已知四边形ABCD为平行四边形,AD⊥BD,AC交BD于0,AD=8,AB=1O,求BC,CD,OC的长. 推理填空:
推理填空: