题目内容
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+x+2
x2+x+2![]() 与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
(1)求点D的坐标及直线AD的解析式;
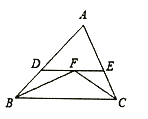
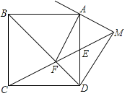
(2)如图1,连接CD、AD、BD,点M为线段CD上一动点,过M作MN∥BD交线段AD于N点,点P是y轴上的动点,当△CMN的面积最大时,求△MPN的周长取得最小值时点P的坐标;
(3)如图2,线段AE在第一象限内交BD于点E,其中tan∠EAB=![]() ,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.

【答案】(1)D(![]() ,2
,2![]() );直线AD解析式y=x+
);直线AD解析式y=x+![]() ;(2)P(0,
;(2)P(0,![]() );(3)G(
);(3)G(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
(1)根据题意可得A,B,C坐标,根据对称可求D点坐标,用待定系数法可求AD解析式;(2)作DH⊥AB,MT⊥AB,交AD于T,作NK⊥MT,设M(m,2![]() ),则T(m,m+
),则T(m,m+![]() ),根据相似三角形可得MK=
),根据相似三角形可得MK=![]() MT,用m表示△CMN的面积,根据二次函数的最值问题,可求M点坐标,作M关于y轴对称点M1(-
MT,用m表示△CMN的面积,根据二次函数的最值问题,可求M点坐标,作M关于y轴对称点M1(-![]() ,2
,2![]() ),连接M1N交y轴于点P,利用待定系数法确定函数关系式以及直线与坐标轴的交点的求法求得点P的坐标;(3)如图3,4,5,分类讨论,通过数量关系列出方程,可求G点坐标.
),连接M1N交y轴于点P,利用待定系数法确定函数关系式以及直线与坐标轴的交点的求法求得点P的坐标;(3)如图3,4,5,分类讨论,通过数量关系列出方程,可求G点坐标.
(1)令x=0,则y=2![]() ,
,
∴C(0,2![]() ),
),
∵对称轴为x=![]() ,且C,D关于对称轴对称,
,且C,D关于对称轴对称,
∴D(![]() ,2
,2![]() ).
).
令y=0,则0=﹣![]() x2+x+2
x2+x+2![]() ,
,
∴x1=﹣![]() ,x2=2
,x2=2![]() ,
,
∴A(﹣![]() ,0),B(2
,0),B(2![]() ,0),
,0),
设直线AD解析式y=kx+b,
![]() ,
,
解得:k=1,b=![]() ,
,
∴直线AD解析式y=x+![]() ;
;
(2)如图1:作DH⊥AB,MT⊥AB,交AD于T,作NK⊥MT
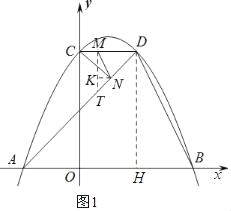
设M(m,2![]() ),则T(m,m+
),则T(m,m+![]() )
)
∵A(﹣![]() ,0),D(
,0),D(![]() ,2
,2![]() ),
),
∴AH=DH
∴∠DAH=∠ADH=45°=∠CDA
∵MT∥DH,KN∥CD
∴∠KNT=∠KTN=45°=∠CDA
∴KT=KN,MT=MD
∵MN∥BD,
∴∠MND=∠ADB且∠CDA=∠DAB
∴△ADB∽△MND,
∴![]() ,
,
∴ND=![]() MD.
MD.
∵DT=![]() MD,
MD,
∴NT=![]() MD.
MD.
∵KN∥CD,
∴![]() ,
,
∴KT=![]() MT
MT
∴KM=![]() MT=
MT=![]() (
(![]() ﹣m)
﹣m)
∴S△CMN=![]() CM×KM=
CM×KM=![]() m×
m×![]() (
(![]() ﹣m)=﹣
﹣m)=﹣![]() m2+
m2+![]() m
m
∴当m=![]() 时,S△CMN最大值.
时,S△CMN最大值.
∴M(![]() ,2
,2![]() ).
).
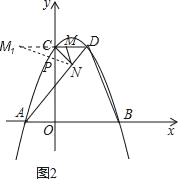
如图2 作M关于y轴对称点M1(﹣![]() ,2
,2![]() ),
),
由B(2![]() ,0),D(
,0),D(![]() ,2
,2![]() )得到直线BD的解析式为:y=﹣2x+4
)得到直线BD的解析式为:y=﹣2x+4![]() .
.
∵MN∥BD,
∴设直线MN的解析式为:y=﹣x+t.
把M(![]() ,2
,2![]() )代入求得:y=﹣x+
)代入求得:y=﹣x+![]() .
.
联立方程组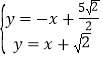 ,
,
解之得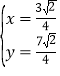 ,即N(
,即N(![]() ),
),
由M1(﹣![]() ,2
,2![]() ),N(
),N(![]() )得到直线M1N的解析式为:y=﹣
)得到直线M1N的解析式为:y=﹣![]() x+
x+![]() .
.
令x=0,则y=![]() ,即:P(0,
,即:P(0,![]() ).
).
(3)如图3:

①当AG=FG,∠GFB=90°时,∵tan∠EAB=![]() ,
,
∴设FH=a,则AH=2a,设AG=FG=x,则GH=2a﹣x
∵FH2+GH2=FG2
∴a2+(2a﹣x)2=x2
∴x=![]() a,
a,
∴GH=![]() a,
a,
∵FH⊥AB,GF⊥FB
∴∠FBG=∠GFH
∴tan∠GFH=tan∠FBG
∴![]() ,
,
∴BH=![]() a
a
∵AH+BH=AB=3![]() ,
,
∴2a+![]() a=3
a=3![]() ,
,
∴a=![]() ,
,
∵OG=AG﹣AO
∴OG=![]() ×
×![]() ﹣
﹣![]() =
=![]() ,
,
∴G(![]() ,0)
,0)
②如图4
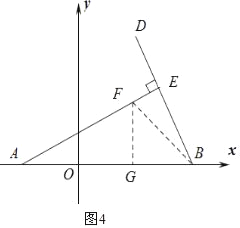
当FG=BG,∠AGF=90°时,设GF=a,则AG=2a,BG=a,
∴AB=AG+BG=3a=3![]() ,
,
∴a=![]() ,
,
∴G(![]() ,0);
,0);
③如图5:
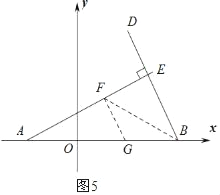
当FG=BG,∠AFG=90°时,设GF=a,则BG=a,AG=![]() a.
a.
∴AB=AG+BG=![]() a+a=3
a+a=3![]() ,
,
∴a=![]() ,
,
∵OG=AG﹣AO=![]() a﹣
a﹣![]() =
=![]() ,
,
∴G(![]() ,0),
,0),
综上所述G(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).

【题目】某科研小组获取了声音在空气中传播的速度v与空气温度t关系的一些数据如下表:
温度t(°C) | -20 | -10 | 0 | 10 | 20 | 30 |
声速v(m/s) | 318 | 324 | 330 | 336 | 342 | 348 |
(1)根据表中提供的信息,可推测速度v是温度t的一次函数,请你写出其函数表达式;
(2)当空气温度为25°C,声音10秒可以传播多少米?