题目内容
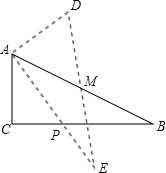
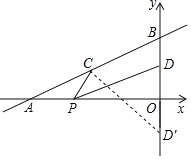
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )

A.(﹣1,0)B.(﹣2,0)C.(﹣3,0)D.(﹣4,0)
【答案】B
【解析】
根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图.
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() x+4中y=0,则
x+4中y=0,则![]() x+4=0,解得:x=﹣8,
x+4=0,解得:x=﹣8,
∴点A的坐标为(﹣8,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣4,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣4,2),D′(0,﹣2),
∴![]() ,解得:
,解得:![]() ,
,
∴直线CD′的解析式为y=﹣x﹣2.
令y=0,则0=﹣x﹣2,解得:x=﹣2,
∴点P的坐标为(﹣2,0).
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商店一周内甲、乙两种计算器每天的销售量如下(单位:个):
类别/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均数 |
甲 |
|
|
|
|
|
|
| |
乙 |
|
|
|
|
|
|
|
|
(1)将表格填写完整.
(2)求甲种计算器本周销售量的方差.
(3)已知乙种计算器本周销售量的方差为![]() ,本周哪种计算器的销售量比较稳定?说明理由.
,本周哪种计算器的销售量比较稳定?说明理由.