题目内容
【题目】直线y=2x+3与抛物线y=ax2交于A、B两点，已知点A的横坐标为3．
（1）求A、B两点的坐标及抛物线的解析式；
（2）O为坐标原点，求△AOB的面积．
【答案】（1）A（3，9），B（﹣1，1），y=x2；（2）6.
【解析】
（1）利用待定系数法即可解决问题；
（2）利用分割法求出△ABO的面积即可.
（1）∵点A的横坐标为3，
∴y=2×3+3=9，
∴点A的坐标是（3，9）
把A（3，9）代入y=ax2中，得：a=1，
∴抛物线的解析式是：y=x2
根据题意，得：
,解得：
或
,
∴点B的坐标是（﹣1，1），
（2）设直线y=2x+3与y轴交于点C，则点C的坐标是（0，3）
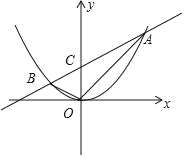
∴△AOB的面积=S△OBC+S△AOC＝
×3×(3+1)＝6．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
