题目内容
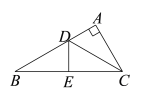
【题目】如图,在△ABC中,∠A=90°,CD是∠ACB的平分线, DE垂直平分BC,若DE=2,则AB=___________.
【答案】6
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得BD=CD,再根据等边对等角求出∠C=∠CBD,根据角平分线的定义可得∠ACD=∠BCD,从而求出∠ABC=∠BCD=∠ACD,然后根据直角三角形两锐角互余求出∠B=30°,根据角平分线上的点到角的两边的距离相等可得AD=DE,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
∵DE垂直平分BC,
∴BD=CD,
∴∠B=∠BCD,
∵CD为∠ACB的平分线,
∴∠ACD=∠BCD,
∴∠ACD=∠BCD=∠B,
∵∠A=90°,
∴∠B=![]() ×90°=30°,
×90°=30°,
∵CD为∠ACB的平分线,∠A=90°,DE⊥BC,
∴AD=DE=2,
∴BD=2DE=2×2=4.
∴AB=AD+BD=2+4=6.
故答案为:6.

练习册系列答案
相关题目