题目内容
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.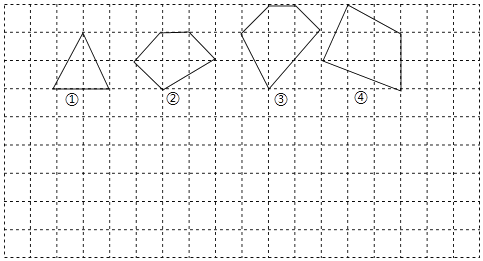
(1)根据图中提供的信息填表:
格点多边形各边上的 | 格点边多边形内部的 | 格点多边形的面积 | |
多边形1 | 4 | 1 | 2 |
多边形2 | 5 | 2 | ② |
多边形3 | 6 | 3 | 5 |
多边形4 | ① | 4 |
|
一般格点多边形 | m | n | S |
则S=(用含m、n的代数式表示)
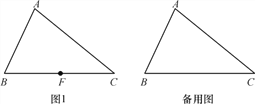
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=(用含m、n的代数式表示).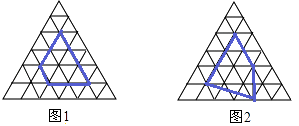
【答案】
(1)![]() ,5,S=
,5,S= ![]() m+n﹣1
m+n﹣1
(2)m+2(n﹣1)
【解析】解:(1)多边形2的面积= ![]() ×1+
×1+ ![]() ×3×1=
×3×1= ![]() ,多边形4的边上的格点数的和为5,
,多边形4的边上的格点数的和为5,
因为2= ![]() ×4+1﹣1;
×4+1﹣1; ![]() =
= ![]() ×5+2﹣1;5=
×5+2﹣1;5= ![]() ×6+3﹣1;
×6+3﹣1; ![]() =
= ![]() ×5+4﹣1,
×5+4﹣1,
所以S= ![]() m+n﹣1,
m+n﹣1,
所以答案是: ![]() ,5,S=
,5,S= ![]() m+n﹣1;(2)因为图1中,m=8,n=1,S=8,8=8+2(1﹣1),图2中,m=7,n=3,S=11,11=7+2(3﹣1),
m+n﹣1;(2)因为图1中,m=8,n=1,S=8,8=8+2(1﹣1),图2中,m=7,n=3,S=11,11=7+2(3﹣1),
所以S=m+2(n﹣1).
所以答案是:m+2(n﹣1).

练习册系列答案
相关题目