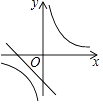
题目内容
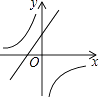
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是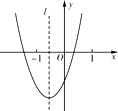
A.a<0
B.c>0
C.a+b+c>0
D.b2-4ac<0
【答案】C
【解析】解:由抛物线开口向上,得a>0,故A错误;
由抛物线与y轴的交点在y轴负半轴,得c<0,故B错误;
当x=1时,y=a+b+c,而由图象可得(1,a+b+c)在第一象限,所以a+b+c>0,故C正确;
由抛物线与x轴有两个交点,则当y=0,即方程ax2+bx+c=0,的判别式b2-4ac>0,故D错误.
故选C.
【考点精析】掌握二次函数的图象和二次函数图象以及系数a、b、c的关系是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).

【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.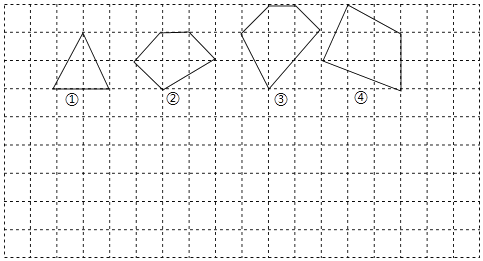
(1)根据图中提供的信息填表:
格点多边形各边上的 | 格点边多边形内部的 | 格点多边形的面积 | |
多边形1 | 4 | 1 | 2 |
多边形2 | 5 | 2 | ② |
多边形3 | 6 | 3 | 5 |
多边形4 | ① | 4 |
|
一般格点多边形 | m | n | S |
则S=(用含m、n的代数式表示)
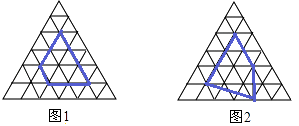
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=(用含m、n的代数式表示).